無料ダウンロード y=x^2 2x-8 in vertex form 197086-Y=x^2+2x-8 in vertex form

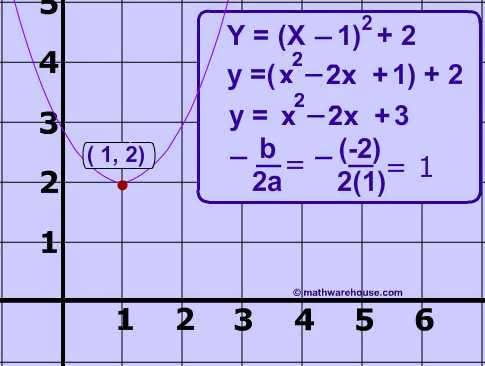
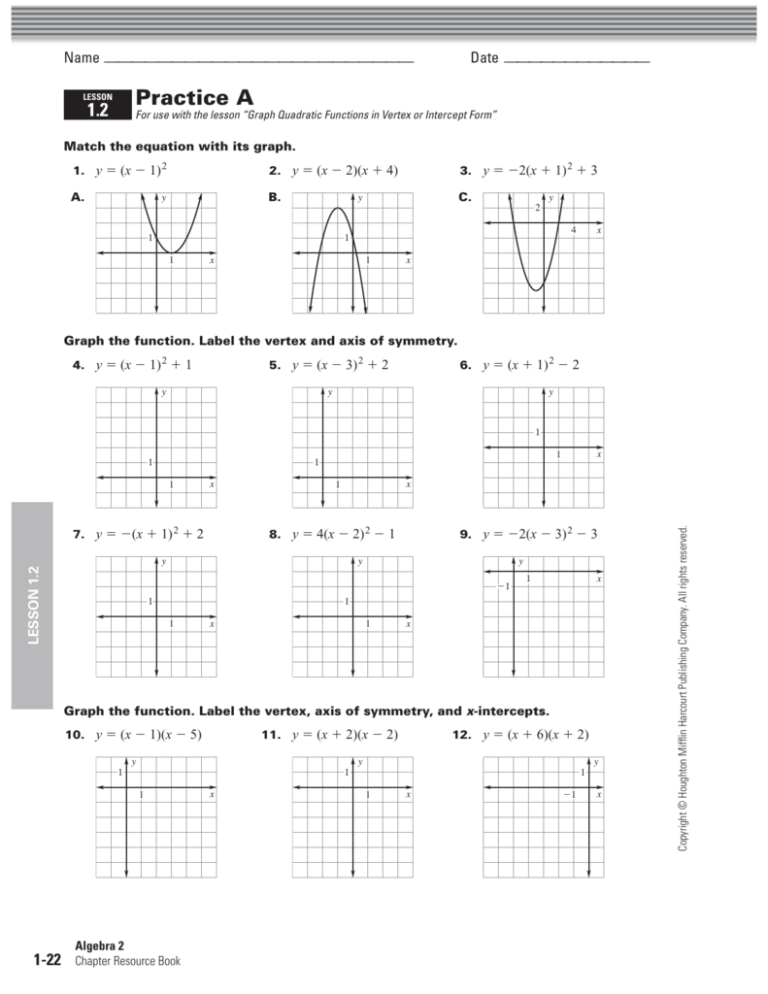
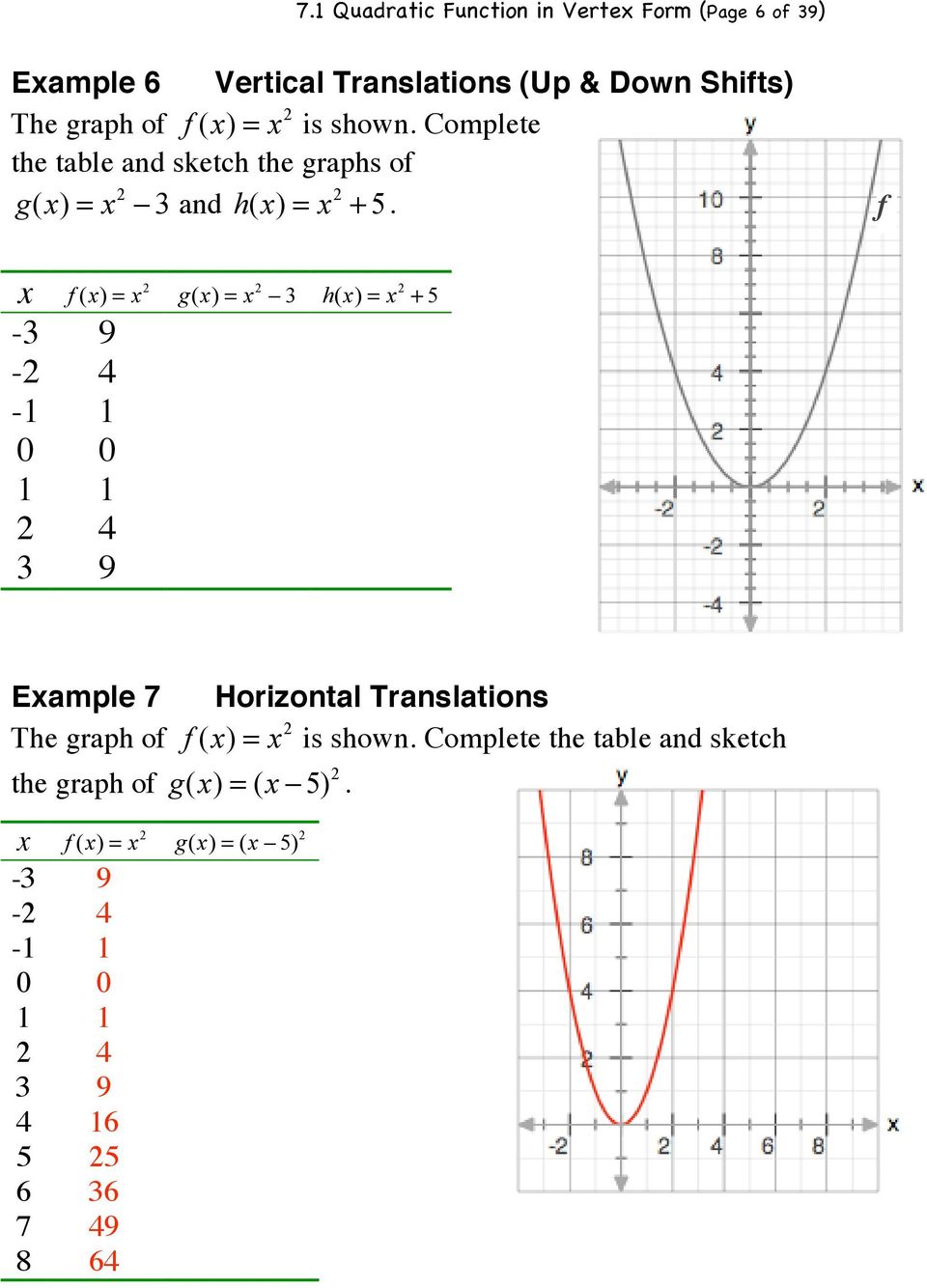
 Method 1 Converting to Vertex Form Vertex form can be represented as #y=(xh)^2k# where the point #(h,k)# is the vertex To do that, we should complete the square #y=x^22x2# First, we should try to change the last number in a way so we can factor the entire thing #=># we should aim for #y=x^22x1# to make it look like #y=(x1)^2# Complete the square to rewrite the quadratic function in vertex form y = x ^ 2 2x 8 Answers 3 Get Other questions on the subject Mathematics Mathematics, 1530, southerntouch103 Gretchen is setting up for a banquet she has 300 chairs and needs to distribute them evenly among t tables how many chairs should she put atLearn to complete the square in order to write quadratic equations in vertex form Click Create Assignment to assign this modality to your LMS We have a new and improved read on this topic

Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube

Y=x^2+2x-8 in vertex form

Y=x^2+2x-8 in vertex form-Create your account View this answer The given equation is y =x2−2x−8 y = x 2 − 2 x − 8 To convert this into the vertex form, we have to complete the squares Adding 8 8 on both sidesPlug (1,7) into the equation and define b in terms of a math7=ab8\\b=a1/math (0,8) is a point on the parabola, so by symmetry, (2,8) is also a point Plug (2,8) into the equation and define b in terms of a math8=4a2b8\\b=2a\\/math

Vertex Form Of Quadratic Functions Math 2 Y

Divide 22\sqrt {y} by 2 The equation is now solved Swap sides so that all variable terms are on the left hand side Factor x^ {2}2x1 In general, when x^ {2}bxc is a perfect square, it can always be factored as \left (x\frac {b} {2}\right)^ {2} Take the square root of1) y=(x−17)(x2) 2)y=(x−17)(x−2) 3)y=(x−6)2 2 4) y=(x−6)2 −2 6 Which equation and ordered pair represent the correct vertex form and vertex for j(x) =x2 −12x7?My initial idea was to take the derivative, and set it to zero y = x^2 8x 10 dy/dx = 2x 8 Setting that to zero gives an x value of 4, and plugging x = 4 into the first equation gives y = 6 Thus, the ve

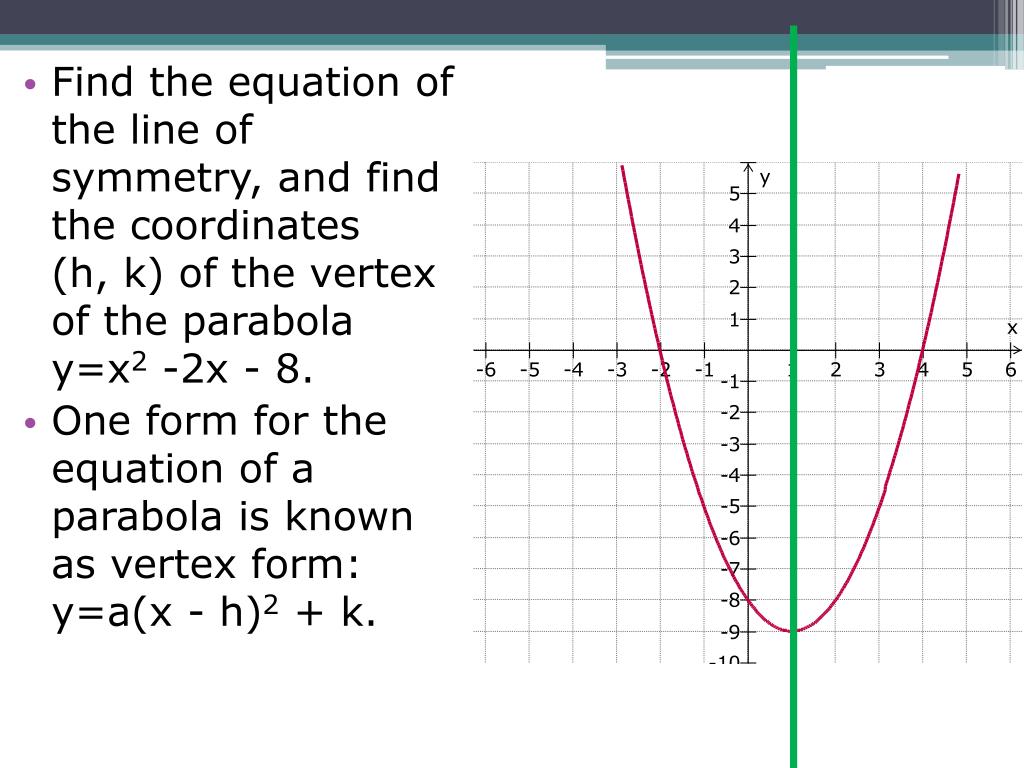
Subtract y from both sides 2x^ {2}8x1y=0 2 x 2 8 x 1 − y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 2 for a, 8 for b, and 1y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0X 2 2x 8 = 0 Step 2 Parabola, Finding the Vertex 21 Find the Vertex of y = x 22x8 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum)Y=x^2−16x63 The vertex has an xvalue of b/2a=(16)/2=8 f(8)= 1 Therefore, the vertex is at (8,1) The vertex form is (xh)^2 k, where you change the sign of the x value of the vertex (h) and keep the y component (k)

Y = x2 − 2x − 8 y = x 2 2 x 8 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 2 x − 8 x 2 2 x 8 Tap for more steps Use the form a x 2 b xFree factor calculator Factor quadratic equations stepbystepYou can put this solution on YOUR website!

Standard Form To Vertex Form Definitions Facts And Solved Examples Cuemath

5 1 Quadratic Functions Mathematics Libretexts

Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution PhysicsIs it ellipse 2 Find the coordinates of the vertex and the equation of the axis of symmetry for the parabola represented by x^2 4x 6y 10 = 0 vertex (2 , 1) axis of Math For each situation first write and equation in the form of y=mx bSolved by pluggable solver Completing the Square to Get a Quadratic into Vertex Form Start with the given equation Subtract from both sides Factor out the leading coefficient Take half of the x coefficient to get (ie ) Now square to get (ie ) Now add and

Y X

2 2 Characteristics Of Quadratic Functions Flip Ebook Pages 1 10 Anyflip Anyflip

 Click here 👆 to get an answer to your question ️ Express the function y = 2x^2 8x 1 in vertex form Explanation y = x2 − 2x 8 or y = (x2 − 2x 1) −1 8 or y = (x − 1)2 7 Comparing with vertex form of equation f (x) = a(x −h)2 k;(h,k) being vertex we find here h = 1,k = 7,a = 1 ∴ Vertex is at (1,7) and vertex form of equation is y = (x − 1)2 7 graph {x^22x8 3554, 3558, 1778, 1778} Ans Answer link Explanation Changing a quadratic function from standard form to vertex form actually requires that we go through the process of completing the square To do this, we need the x2 and x terms only on the right side of the equation y = x2 2x −8 y 8 = x2 2x −8 8 y 8 = x2 2x −8 8 y 8 = x2 2x

Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation

How Do You Graph Y X 2 2x 3 Socratic

The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy8=0 x 2 2 x − y − 8 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and 8y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}Find the Vertex Form y=x^22x1 Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factor ofY = (x 2 2x 8) y = (x 2 2 ⋅ x ⋅1 1 218) y = ((x1) 29) y = (x1) 2 9 By comparing this with the vertex form of parabola, we get (h, k) ==> (1, 9) Example 6 y = (x1)(x3) Solution y = x 24x3 y = x 22 ⋅ x ⋅2 2 22 2 3 y = (x2) 243 y = (x2) 21 By comparing this with the vertex form of parabola, we get

The Vertex Form Of The Function Is Choose The Equation That Shows A Step In The Process Of Brainly Com

How To Graph A Quadratic Equation 10 Steps With Pictures

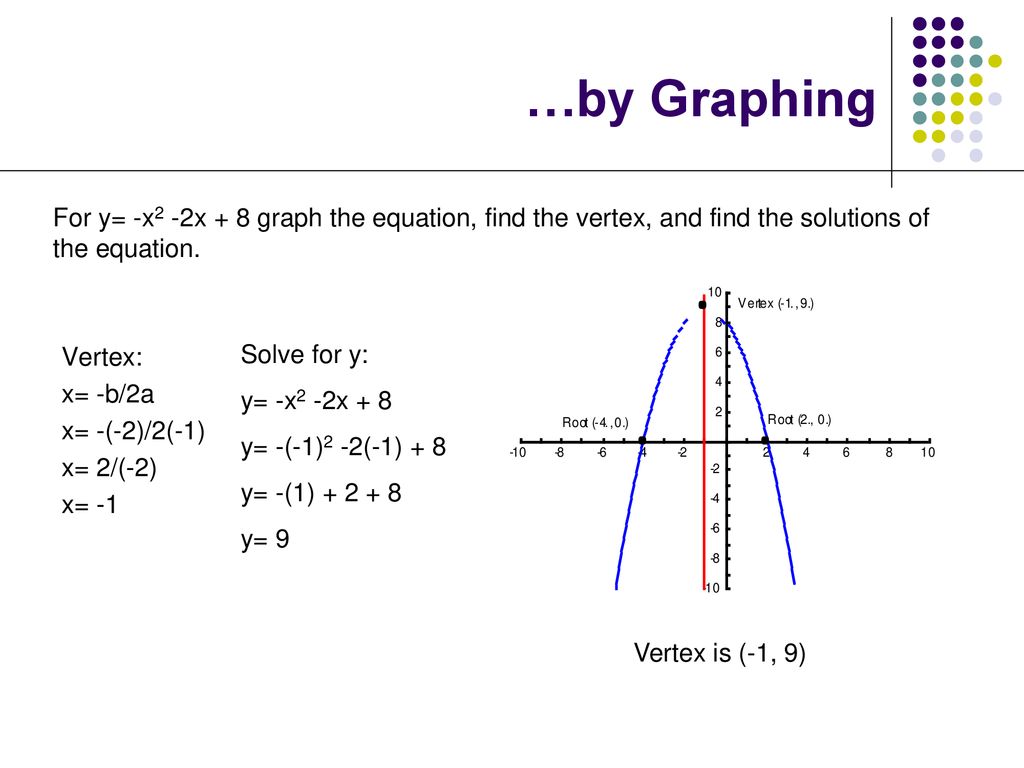
👉 Learn how to graph quadratic equations by completing the square A quadratic equation is an equation of the form y = ax^2 bx c, where a, b and c are c y = x² 4x 12 When y = 0 x² 4x 12 = 0 x² 4x 12 = 0 (x 2)(x 6) = 0 x = 2 or x = 6 The xintercepts are 2 and 6 y = (x² 4x) 12 y = (x² Find the vertex of the function y = –x2 2x 8 It is where the derivative 2x 2 = 0 Since you probably haven't learned about derivatives, do it this way Rewrite is as x^2 2x 8 = (x1)^2 7 Now look at the form of the formula on the right It

Chapter 5 Study Guide

Exploring Quadratic Functions Ppt Download

To find the x intercepts find the zeros of the equation y=x^22x1 = (x1)^2 hence the two intercepts are (1,0), (1,0) The vertex is located when the derivative of the equation is zero, y'=0 y'=2x2 y'=0=2x2 => 2x=2 or x =1 The vertex is aFree functions vertex calculator find function's vertex stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyY=2x^212x14 y=x^2x1 Albebra Find the vertex of the function y = –x2 2x 8 It is where the derivative 2x 2 = 0 Since you probably haven't learned about derivatives, do it this way Rewrite is as x^2 2x 8 = (x1)^2 7 Now look at the form of the formula on

Vertex Form Of Quadratic Functions Math 2 Y

Writing Quadratic Equations Vertex Form To Standard Form Practice Quadratics Quadratic Equation Equations

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreY = x2 ­ 2x ­ 8 Convert to vertex form by completing the square y = 2x2 ­ 12x 6 Equivalent Equations ­ May be asked which equation has the same solution as the equation in the question Convert the quadratic to standard form y = ­(x 2)2 ­ 7 Convert the quadratic to standard formVertex form of a quadratic equation is y=a(xh) 2 k, where (h,k) is the vertex of the parabola;

7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

How To Change A Quadratic Equation From Standard Form To Vertex Form Math Wonderhowto

In vertex form as 1) f(x) =(3x6)2 −25 2) f(x) =3(x6)2 −25 3) f(x) =3(x2)2 −1 4) f(x) =3(x2)2 7 5 Which equation is equivalent to y−34 =x(x−12)? the equation of a parabola in vertex form is ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯∣∣ ∣ 2 2y = a(x − h)2 k2 2 ∣∣ ∣ −−−−−−−−−−−−−−−−−−−−− where (h,k) are the coordinates of the vertex and a is a multiplier given the parabola in standard form;y = ax2 bx c then the xcoordinate of the vertex is ∙Algebra Find the Vertex Form y=x^22x8 y = x2 − 2x − 8 y = x 2 2 x 8 Complete the square for x2 −2x−8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = − 8 a = 1, b = 2, c =

Mfg The Vertex Of A Parabola

1

21 Terms charityjohnson5 Algebra 1 Graphing Quadratics (Vertex & Standard Form) Find the vertex of y = 3 (x 9)^2 1 Find the vertex of y = 1 (x 9)^2 1 Find the vertex of y = 4 (x 7)^2 8 Find the vertex of y = 4 (x 8)^2 7When graphing the parabola in standard form, to find the vertex we use the following method The xvalue of the vertex is calculated as x = b/(2a) The yvalue of the vertex is f(b/(2a)) The xvalue of the vertex also represents the horizontal shift, while the yThe quadratic formula gives two solutions, one when ± is addition and one when it is subtraction 2x^ {2}6xy8=0 2 x 2 6 x − y − 8 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 2 for a, 6 for b, and 8y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}

Symmetry To Plot T Complete The Para 4 Hx X 42 3fx X 3 Y 19 6 Yx 72 1 5 Gx X 32 5 8 Gx 2x

Find Factored Form And Vertex Of F X X 2 2x 8 Youtube

Divide 0 0 by − 8 8 Multiply − 1 1 by 0 0 Add 8 8 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a(x−h)2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k kHow do i convert quadratic functions from standard to vertex form?Parabola, Finding the Vertex 21 Find the Vertex of y = x 214x58 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero)

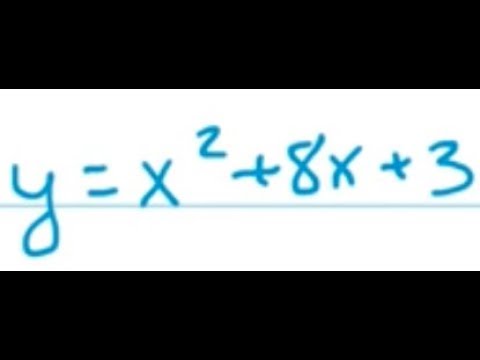
Put Y X 2 8x 3 In Vertex Form Youtube

Transformations Of Quadratic Functions College Algebra

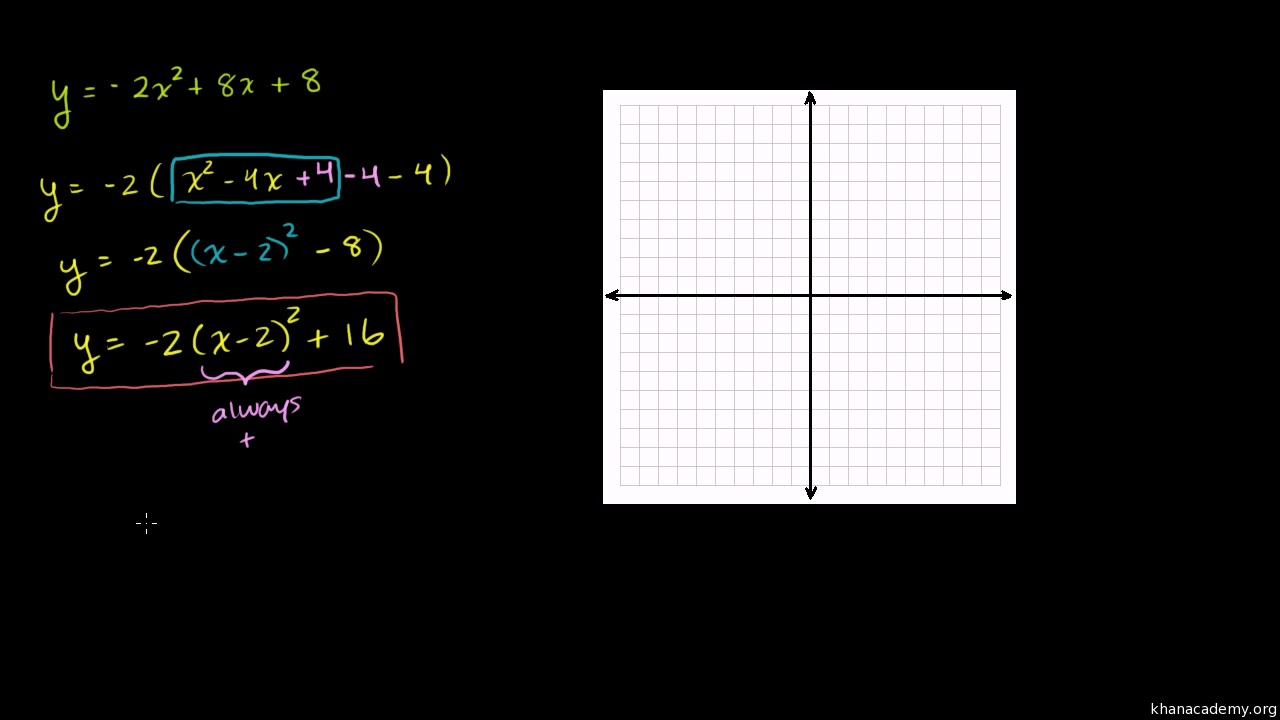
We want to put it into vertex form y=a (xh) 2 k We can convert to vertex form by completing the square on the right hand side Adding 18 to both sides gives us a perfect square trinomial on the right The vertex of a quadratic equation in vertex form is (h,k), so our vertex is (3,22) The equation is y = x 2 2x 2 To change the expression (x 2 2x) into a perfect square trinomial add (half the x coefficient)² to each side of the expression Here x coefficient = 2 So, (half the x coefficient) 2 = (2/2) 2 = 1 Add and subtract 1 to the expression y = (x 2 2x 2 1 1) y = (x 2 2x 1 2 1) y = (x 2 2x 1 3) y = (x 2 2(1)(x) 1 ²) 3The two answers below are perfect;

Parabolas In Standard Intercept And Vertex Form Video Lesson Transcript Study Com

How To Go From Standard Form To Vertex Form By Completing The Square

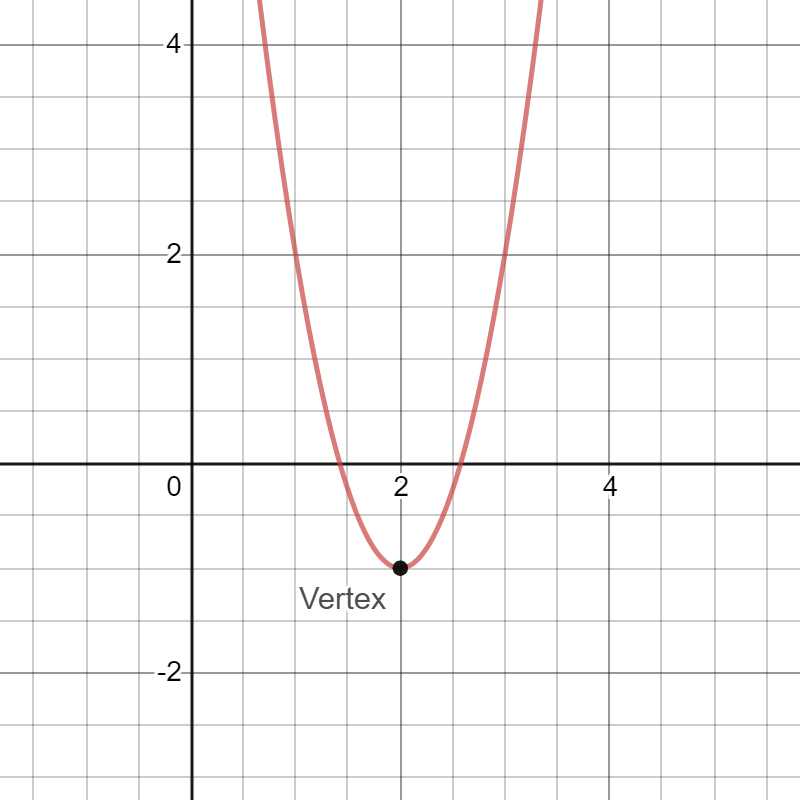
 Vertex Form Of A Quadratic The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertexThe "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or opens downThink of it this way A positive "a" draws a smiley, and a negativeThe vertex form is a special form of a quadratic function From the vertex form, it is easily visible where the maximum or minimum point (the vertex) of the parabola is The number in brackets gives (trouble spot up to the sign!) the xcoordinate of the vertex, the number at the end of the form gives the ycoordinate This means If the vertex form is , then the vertex is at (hk) How to put a function into vertex form?1 Identify the conic section represented by 9y^24x^2 108y24x= 144?

Quadratic Functions

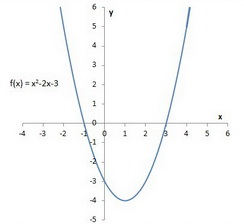
How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic

But the equation for a parabola can also be written in "vertex form" y = a ( x − h) 2 k In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, yThe vertex of an equation in vertex form is (h,k), which for our equation is (6,4) Notes Right now our quadratic equation, y=x 2 12x32 is in standard form xintercepts x^2 8x 12 = 0 (x 6)(x 2) = 0 x 6 = 0 or x 2 = 0 x = 6 or x = 2 Vertex The formula for the parabola with vertex (h,k) is y = a(x h)^2 k Complete the square y = x^2 8x 12 = x^2 8x 16 12 16 = (x 4)^2

How To Write The Equation Of The Parabola In Vertex Form Quora

What Is The Equation Of The Following Graph In Vertex Form Y X 3 2 1 Y X 3 2 1 Y Brainly Com

 which is in vertex form The graph of this equation is a parabola that opens upward It is translated 2 units to the left and 3 units upward This is the advantage of vertex form The transformations required to draw the graph of the function are easy to spot when the equation is written in vertex formVertex Form Equation & Functions Just as y = mx b is a useful format for graphing linear functions, y = a(x h)^2 k is a useful format for graphing quadratic functions If the equation has the form y = ax 2 bx c, the xcoordinate of the vertex is x = b/(2a) For the problem y = x 2 2x 8, a = 1, b = 2, and c = 8, so, the xcoordinate of the vertex is x = 2/2 or 1

Biomath Quadratic Functions

Solution Use The Graph Of Y X 2 2x 8 Does This Function Have A Maximum And Minimum And If So What Are They

Select a few x values, and plug them into the equation to find the corresponding y values The x values should be selected around the vertex Tap for more steps Replace the variable x with 0 in the expression f ( 0) = − ( 0) 2 2 ( 0) − 8 Simplify the resultThe vertex of a parabola is the point at the top or bottom of the parabola 'h' is 6, the first coordinate in the vertex 'k' is 4, the

Vertex Form Request Y X 2 14x 11 Youtube

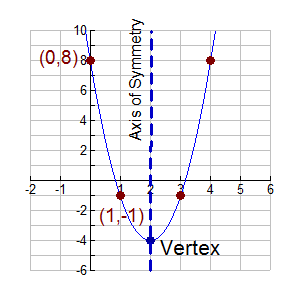
Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math

Quadratic Equations And Quadratic Functions On The Sat

Axis Of Symmetry

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21

Untitled Document

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21

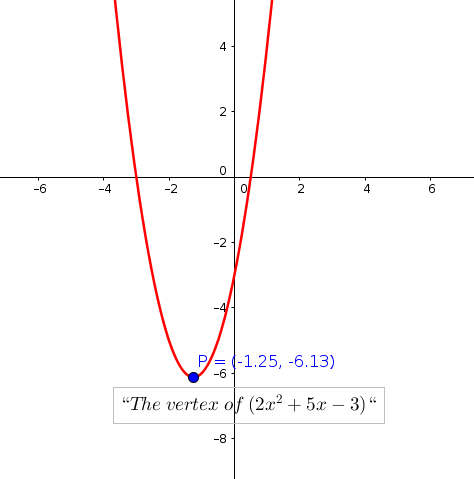
What Is The Vertex Form Of Y 2x 2 5x 3 Socratic

Converting Quadratic Equations Worksheet Coach Forrester

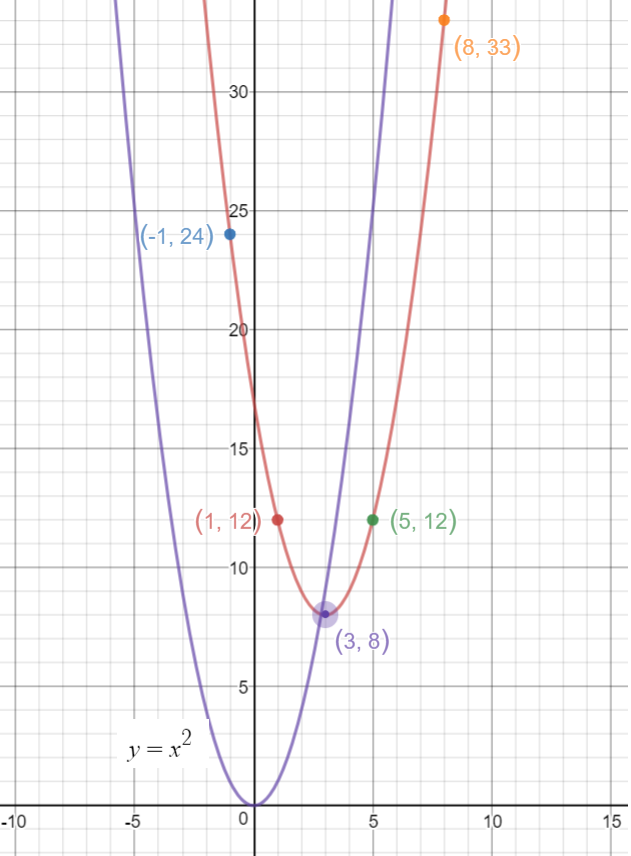
Vertex Form Of A Quadratic Equation Algebra Socratic

Graphing Quadratic Functions

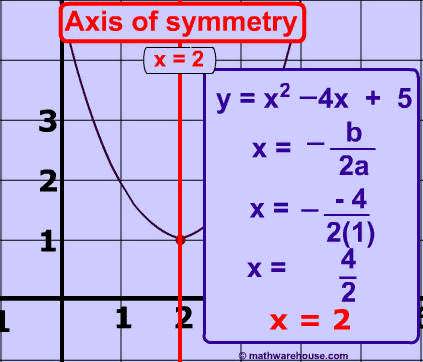
How To Convert Equation Of Parabola From Vertex To Standard Form And From The Standard Equation To Vertex Form

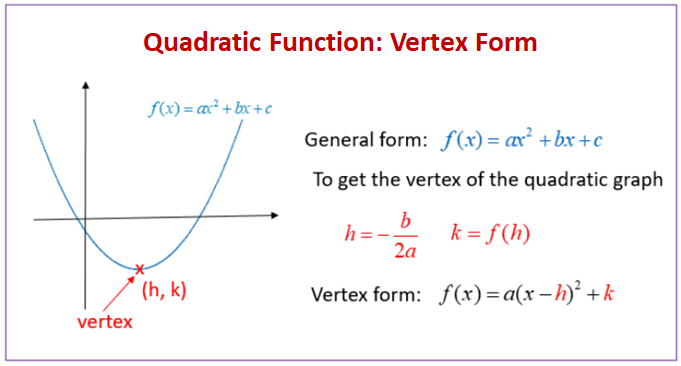
Quadratic Functions Examples Solutions Videos

Biomath Quadratic Functions

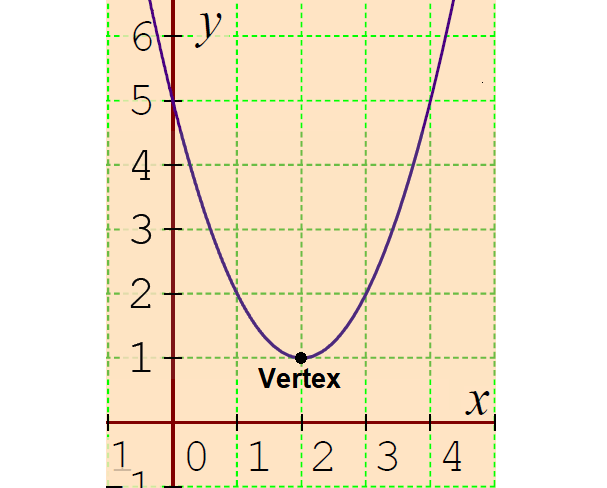
Vertex Form Of A Quadratic Equation

How To Graph A Quadratic Equation 10 Steps With Pictures

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21

2

2 C U K2f0w1c2k Akduote

Q Tbn And9gcrp9hpi7emwokn0e2fajh3aom0rmz7yizyhaftxq5127se4oc4j Usqp Cau

Quadratic Functions Precalculus I

4 1 Linear Applications Phone Charges The Monthly

How To Convert Equation Of Parabola From Vertex To Standard Form And From The Standard Equation To Vertex Form

7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip

Vertex Intercept And Standard Form Ck 12 Foundation

Solution Write Each Function In Vertex Form Sketch The Graph Of The Function And Label Its Vertex 33 Y X2 4x 7 34 Y X2 4x 1 35 Y 3x2 18x 36 Y 1 2x2 5x

6 3 Interpreting Vertex Form And Standard Form

Www Pittsfordschools Org Cms Lib Ny Centricity Domain 1335 homelearningquad1alg Pdf

Standard 9 Write A Quadratic Function In Vertex Form Ppt Video Online Download

Graph The Quadratic Function Y X 2 2x 3 Vertex X Y Intercepts Symmetry Domain Range Youtube

5 Write The Equation Of The Parabola In Vertex Form Chegg Com

Characteristics Of Quadratic Functions Math 1 Eoct Review

5 1 What You Should Learn

Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube

Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

Complete The Square Lesson Ppt Download

Quadratic Equations And Quadratic Functions On The Sat

Ppt Building Understanding For Quadratics Powerpoint Presentation Free Download Id

Quadratic Functions

Finding Features Of Quadratic Functions Video Khan Academy

Graphing Quadratic Functions

Graphing Parabolas

Changing Quadratic Functions From Standard Form To Vertex Form Flashcards Quizlet

2

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

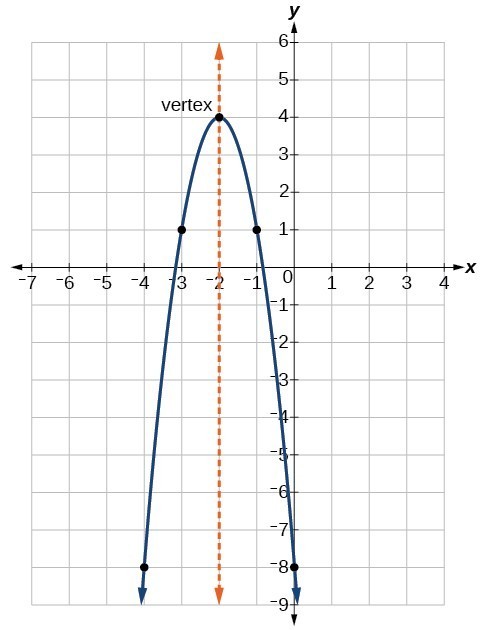
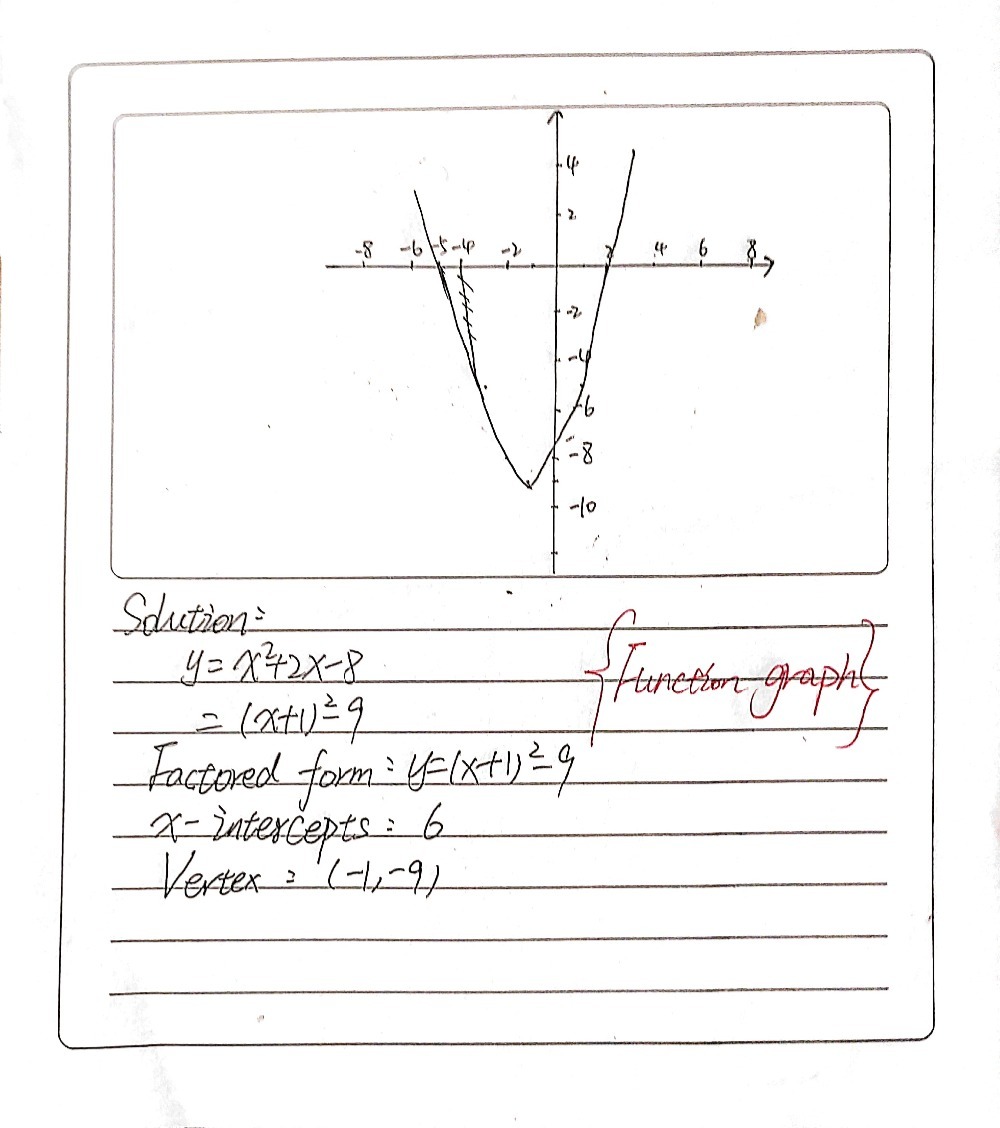
Write The Equation In Vertex Form Y X 2 2x 8 Study Com

Example 4 Write A Quadratic Function In Vertex Form Write In Vertex Form Then Identify The Vertex X 2x 2 10x 22 Y Solution X 2x 2 10x 22 Y Write Ppt Download

25 Best Memes About Vertex Form Vertex Form Memes

7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip

Vertex Form Vertex Form Vertex Form Is Another

1

Quadratic Functions

Solution What Is The Vertex Form Of F X X 2 2x 5

Zzjkxlptghf5mm

What Would An Equation For A Quadratic Function In Vertex Form With Vertex 1 6 That Passes Through The Point 3 4 Be Quora

7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

Http Www Mrsfruge Com Uploads 1 2 0 0 P2a 3 3 Quadratic Functions Packet Pdf

5 3 Vertex Form Of Quadratic Functions Translating Pages 1 4 Flip Pdf Download Fliphtml5

Forms Of Quadratics Explanations Tips And Examples Albert Resources

To Find The Vertex Transform The Quadratic Function From Standard Form To Vertex Form By Completing The Square Y 2x2 12x 10 2x2 6x 10 2x2 6x 9 18 10 2328 Square Meme On Awwmemes Com

3 Vertex Form

Olma Org Ourpages Auto 18 10 4 2 5 answers Pdf

Converting Quadratic Equations Ppt Download

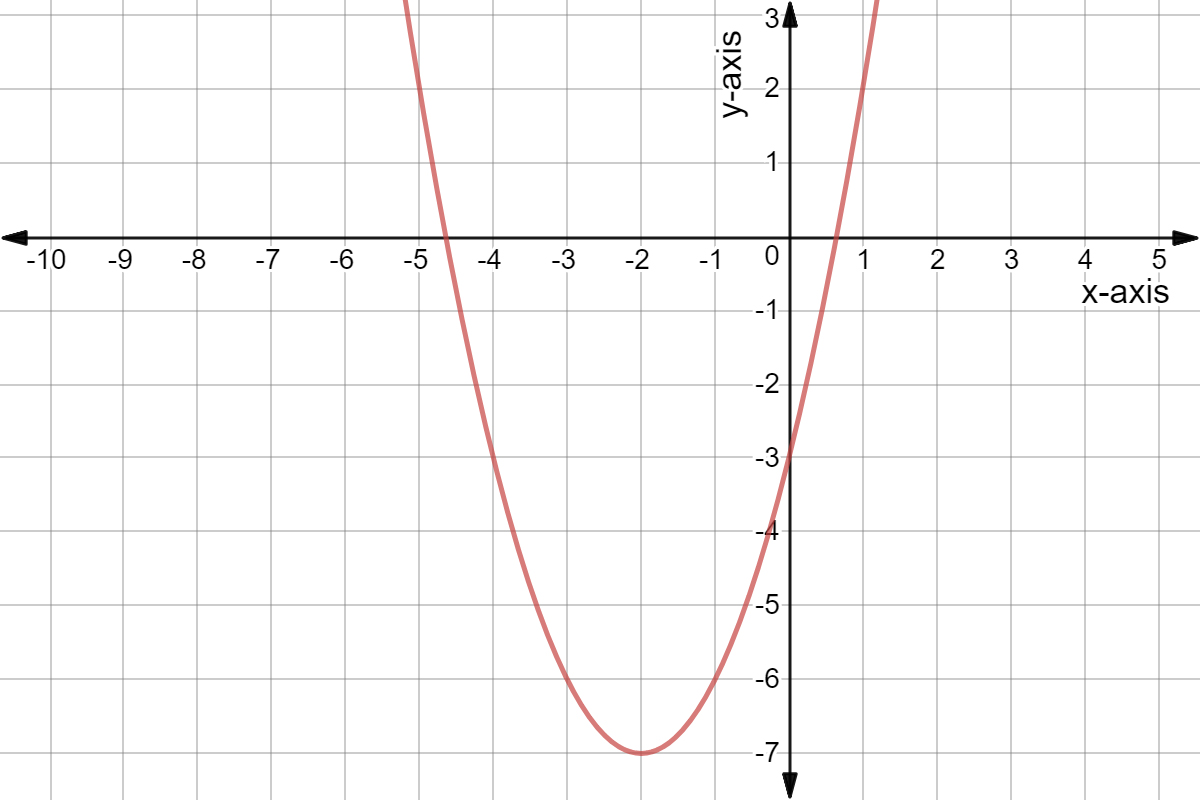
What Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic

Completing The Square Vertex Form Of A Quadratic Expii

Write Each Quadratic Function In Standard Form And Chegg Com

Http Www Midwayisd Org Cms Lib Tx Centricity Domain 164 Preap alg ii 4 7b Pdf

Fireworks From Standard To Vertex Form Ppt Video Online Download

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora

View Question What Is The Vertex Of The Equation Y X 2 2x 8

Y Graph The Following Quadratic Function Y X2 2 Gauthmath

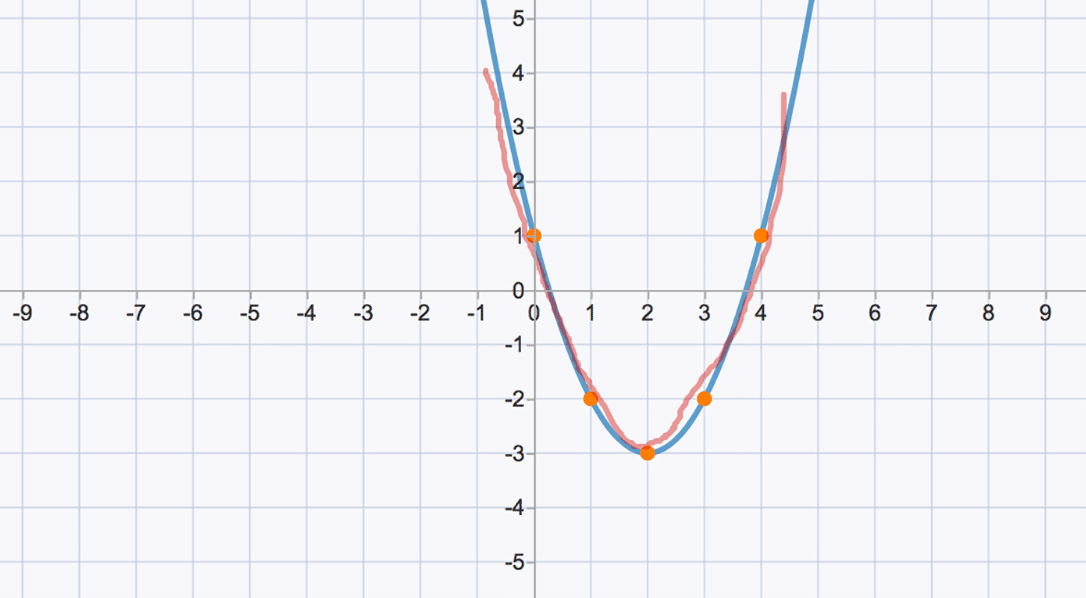
What Is Vertex Form Example Get Education

Answered Put The Quadratic Into Vertex Form And Bartleby

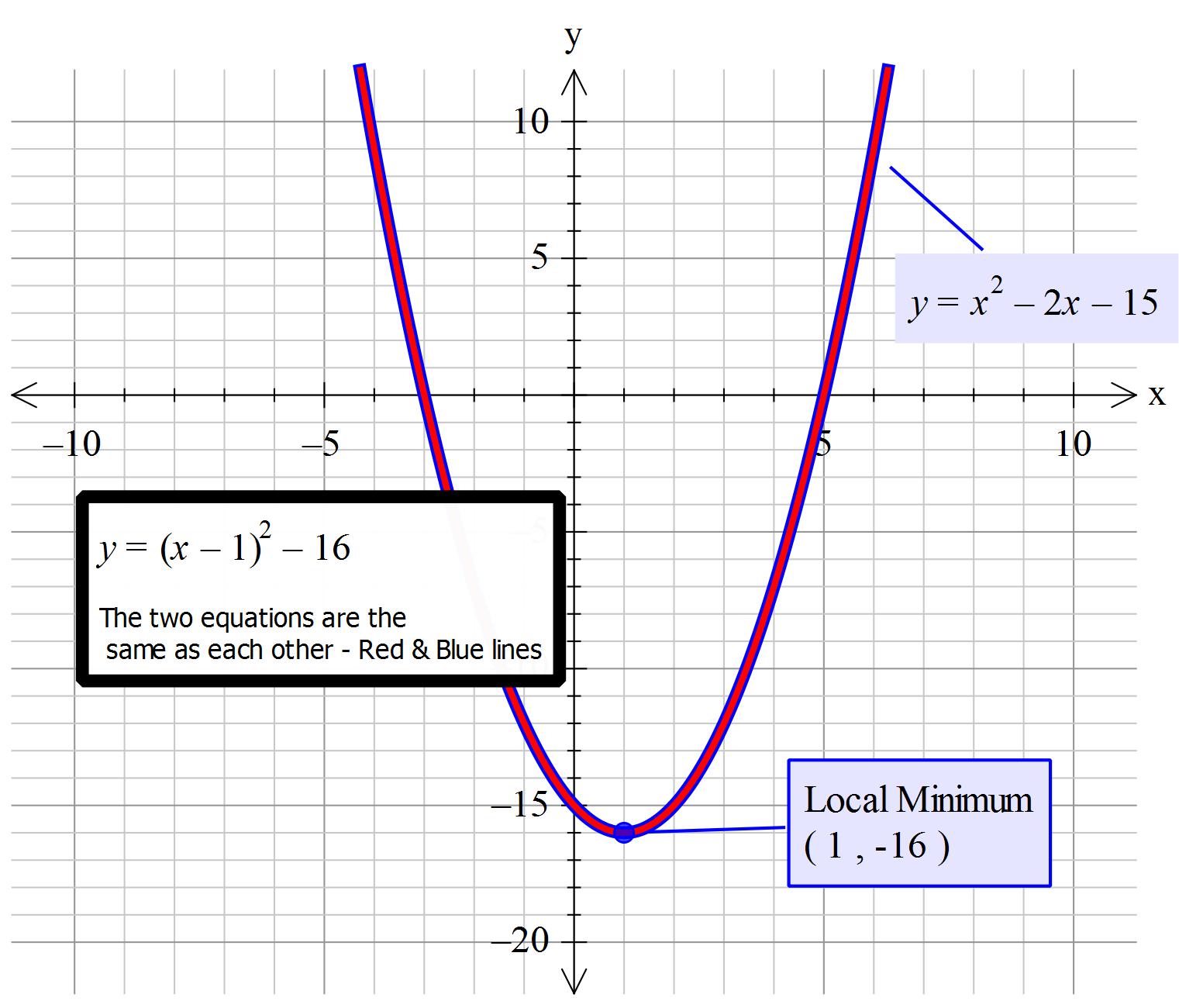
What Is The Vertex Form Of Y X 2 2x 15 Socratic

Http Msflowersmath Weebly Com Uploads 2 7 8 6 10 8 Algebra Cw Pdf

Incoming Term: y=x^2+2x-8 in vertex form,