下記の3元連立1次方程式を考えよう。 (変数は x 1, x 2, x 3) 5x 1 3x 2 x 3 = 3 4x 1 5x 2 2x 3 = 4 x 1 3x 2 6x 3 = 6 とおき、マトリックスで表記すると、極めて簡単に三元連立方程式 自分の計算が不安で利用させていただきました。 思っていたより間違ってたので使ってよかったです。 4元にも対応してくれたら大変有難いです。 世界の経緯度観測所のデータ(3か所)から、形状軸からの極 (瞬間自転軸)のズレの計算に213 連立代数方程式 一松 第3章 6節「連立代数方程式」の写経。 計算機代数の話題はまだ数多くあるが、近年有名になった「グレブナー基底」に ついて略説する。 多変数多項式に関する連立代数方程式を解く問題は良く現れるが、 一般的な解法はほとんど
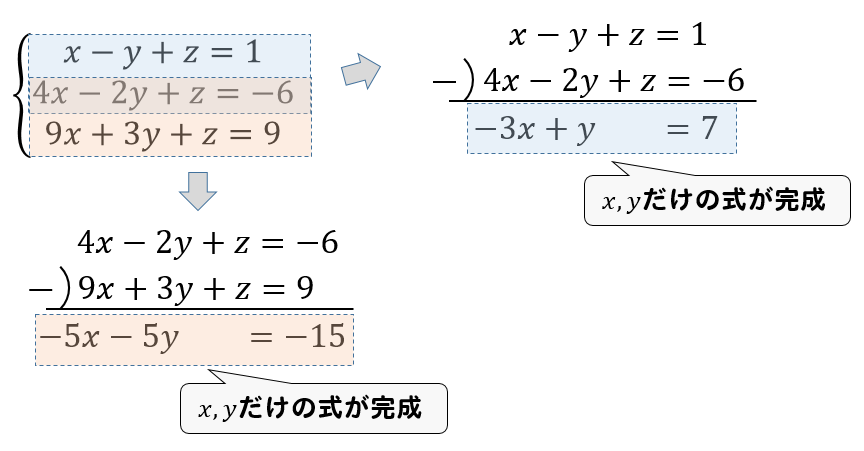
連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト
3連立方程式 エクセル
3連立方程式 エクセル-連立1次方程式の解き方 未知数がn個 x 1, x 2, x 3, ··, x n ,方程式がn個の連立1次方程式 は,行列を用いて のように書くことができる.この連立方程式を係数行列 A を用いて A =― 1 ― 1 次の⑴~⑶にあてはまるものを,下の㋐~㋓の中からすべて選びなさい。 ⑴ 2元1次方程式3x+4y=1の解 x ⑵ 2元1次方程式2−y=8の解 ⑶ 連立方程式 の解




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook
「連立方程式の解」とは,左の例 (A) などにおいて2つの方程式を両方とも満たす x , y の値のことです. 連立方程式の解を求めるには,まず,未知数が1つだけ(たとえば x だけ)の方程式を作って,解くことを考えます. x だけの方程式なら解けるからです. 連立方程式 濃度に関する問題その3 濃度に関する問題の3回目です。 今回は、濃度が異なる食塩水を出し入れするという操作がはいる問題です。 3回目の★★★問題には、入試の過去問に基づいた問題を出すつもりでしたが、手持ちの資料の中には濃度まず次の連立方程式を解いてみましょう。これは、二元連立一次方程式です。変数(未知 数)がx とy の二つだからです。右の列に書いたものは、方程式の係数だけを取り出し て書いたものです。 と= は省いてありますが、−3 のところは、(−3) と考えて−3
3つの文字、式の連立方程式を計算する方法 xy=3,xy=2の和と積の連立方程式の解き方は? 途中で速さが変わる文章問題の解き方、コツを解説! 割合を使った全校生徒の増減に関する文章題の解き方を解説! 池の周りを追いつく速さの問題を解説!測定された2波長赤外線カメラ3の出力値をこの関係式に代入し、2元非線形 連立方程式 を解くことにより、目標の温度及び距離を求める。 例文帳に追加 A measured output value from the twowavelength infrared camera 3 is substituted for the relational3元連立方程式、4元連立方程式があります。 経過 10年10月4日 date,10,10,9,a 連立方程式1から3まで作成しました。 date,10,04,29,a 連立方程式4(そろえにくい)を作成しました。 date,14,7,13,a
X=6*y=4 x= 5 2 *y=2 3 x=8*y=12 x= 3 2 *y= 9 4 x=3*y=7 x=5 2 *y=8 3 x=16*y=10 x= 15 2 *y=21 2 x=3*y=6 x=1 4 *y=1 6 x=9*y=12 x=7 6 *y= 9 8 解説 A=B=CをA=C, B=Cの形にして2つの式 を解く前の子に、 「何を消すの?」と聞きます。 この連立方程式を見た子が、 「 y を消す」と答えてくれます。 続いて、 「どのようにするの?」と聞きます。 すると、 「2 番目と 3 番目を足す」ことと、 「3 番目を 2 倍してから、 1 番目に足す」ことを、 答えてくれます。 3元連立微分方程式 dx/dt=xyz① dy/dt=4x3y7z② dz/dt=2xy5z③ の解法 <解法1> ①×2②③をつくってみます。 右辺は、 2x2y2z4x3y7z2xy5z=0




加減




國中數學2 1 2解二元一次聯立方程式
掃き出し法による3元1次連立方程式の解き方の手順 準備が整ったところで、いよいよ3元一次連立方程式の解き方に入ります。 今回は次の3元一次連立方程式を例として解説していきます。 2xy3z=6 x3y2z=1 3x2yz=7 正則行列であるか行列式を求めて確かめるこの頁では,主に連立方程式の「掃き出し法」による解き方(または「行基本変形」による解き方,または「ガウスの消去法」による解き方)を扱います. 全体の流れ 未知数2個,方程式2個のとき 次の連立方程式において,未知数 x を消去し51 2章連立方程式 確認問題3 りんご 4 個とみかん 6 個の代金は1080円, りんご 3 2 610円である。 1 個,みかん 1 個の値段をそれぞれ求めなさい。 りんご〔 〕 みかん〔 〕 確認問題4 次の問に答えなさい。 ⑴ 2 けたの自然数がある。



早急 この未知数3つ式3つの連立方程式解いて下さい 他の方法 Yahoo 知恵袋




連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト
と分かる. 3 4 ガウス・ジョルダン法のc言語の関数 ピボット選択は行わないで,逆行列も求めないのガウス・ジョルダン法で連立方程式を計 算するプログラムを示す.このプログラムの動作は,次の33連立 1 次方程式の基本変形 定義 38(連立 1 次方程式の基本変形) 連立 1 次方程式に対する次のの操作を連立 1 次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加える. 連立 1 次方程式に基本変形をして得られた方程式と元の方程式とは等価な方程式である. この2本の直線の式はそれぞれ、 y=3/2x6 y=1/2x2 です。連立方程式を解くには、PythonのライブラリであるSympyのsolve()関数を使います。Pythonインタプリタで以下のように実行してみると、交点の座標が(2, 3)であることがわかります。
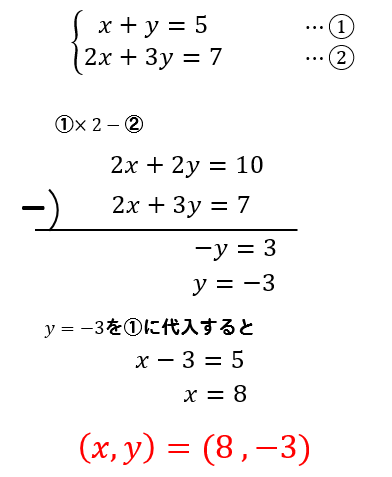



3 Y Shop Clothing Shoes Online



1 3 2 1 4 2 2 15r
微分方程式を離散化して連立一次方程式を生成し、生成された連立一次方程式から行列表示式を生成する(705)。 例文帳に追加 The simultaneous linear equations are formulated by digitizing the differential equation , and a matrix display is formulated from the formulated simultaneous linear連立方程式を解け 3 (2xy)=3x7y23 2 (3x7y)7x=27 7 (x3y)=2 (6x5y)25 11y6 (3x2y)=22 x=5y7 3 (2xy)=4 (x3)24 3 (3xy)=5 (2x3y)15 y=3x5 4x3y=2 (7xy)10 7 (6x1)3 (8y5)=4 2 (5x2y)=3 (4xy)11 4x7y=13 2 (4x3y)=7 (xy)8 3 (x1)=2 (2y9)6 5 (x4y)=2 (2x6y7)13 4x11y=5 (2x3y2)4 5 (2xy7)=2x3y9 7xy5=3 (3x4y14)4 8x=2 連立方程式の裏技です📢 暗算が得意!って方にオススメです☆ 数字が大きいときに使うのは向いていません(1075×16とか出てきても筆算に時間がかかるだけなので)。 でも、すぐに積が分かりそうなら絶対に裏技を使いましょう!時間短縮になりますよ🙌 ぜひ覚えて使ってみてね〜 学年




三元連立方程式 1 中2数学 Youtube
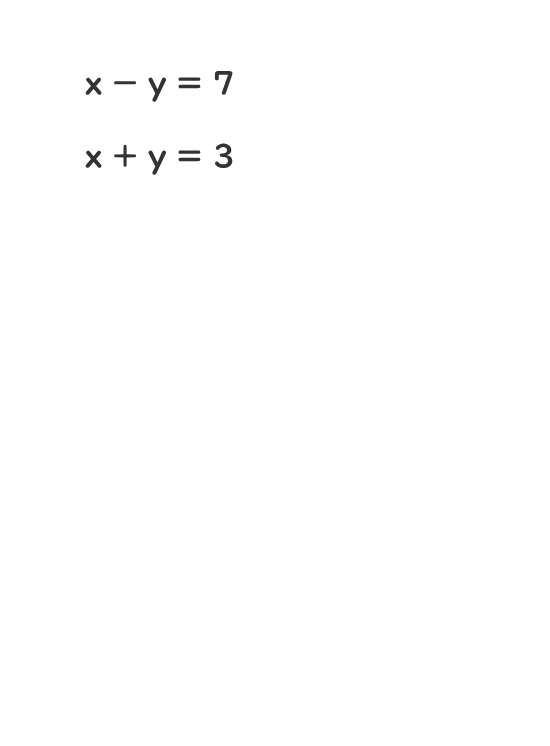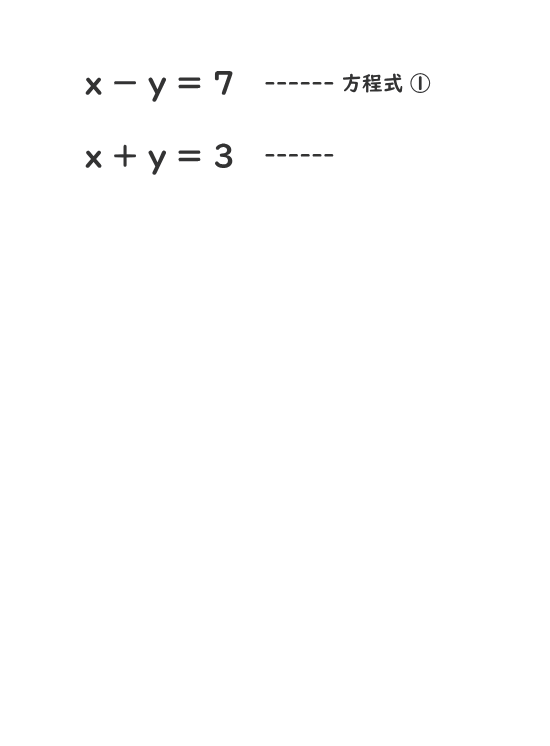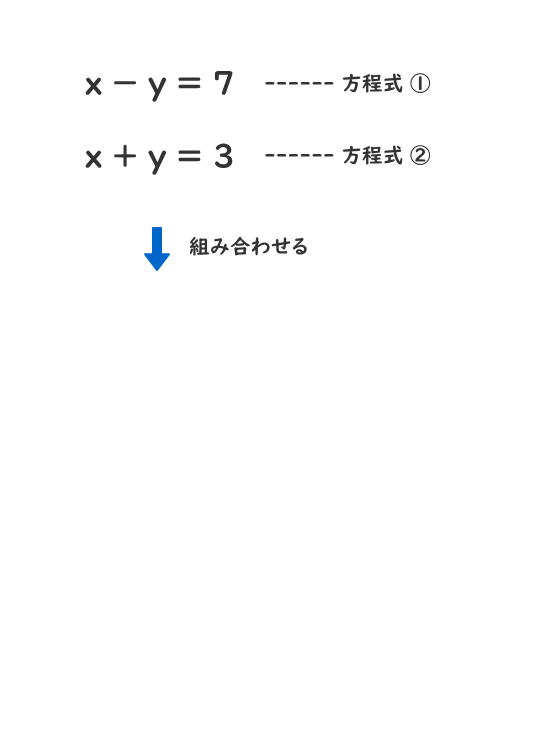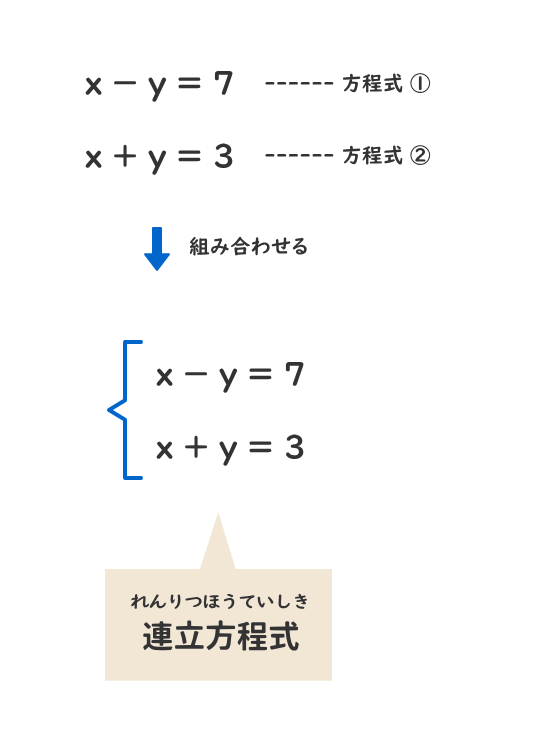



連立方程式の解き方 電験3種web
例3 次の連立1次方程式を考える。 3x1 − 2x2 x3 4x4 = 7 x1 − 3x3 x4 = 5 2x1 − x2 9x3 = 0 この連立1次方程式は、次の行列の方程式でも表される。った(内容的にはGaussJordan の消去法).変形後の連立方程式は最初に与えられた連立方程 式と同値でなければならない.この解法で行うべき操作は,拡大係数行列に対して次のⅠ,Ⅱ, Ⅲを行うことである.これらを行基本変形という. Ⅰ 1つの行に0でない数をかける. 行基本変形 Ⅱ 1つの行にある数をかけて,他の方程式に加える.方程式 1つまたは複数の変数を持つ方程式を解き,グラフを表示してこれを調べる. 一次方程式を解く 4x3=19 整方程式を解く x^2 4x 6 = 0を解く 指定の定義域で解く x^3 4x^2 6x 24 = 0を実数上で解く 方程式をパラメータについて解く




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ




例題 解二元一次聯立方程式 綜合應用1 數學 均一教育平台
中学生の数学連立方程式の利用応用問題の解き方 今回は中学生から質問があった2つの問題を解説していきます。 「人数の割合の問題」と「食塩水 記事を読む 2年生の数学, 連立方程式この漸化式を芋づる式に計算すれば、元の2階の微分方程式の近似解が求められるわけで ある。近似解 は となり、その微分も同時に計算され であ る。 3 2 練習問題 以下の高解常微分方程式を連立1階微分方程式に書き換えなさい。連立方程式をより深く考えるための教材 研究の要約 平井安久* 連立方程式の応用問題として課腰解決的な要瀬を含む教材を作成した連立`元一次方担式 を用いる場面から始まり予想外の解が得られる場面,僻のj勘直を推測する場面,一次関数の




未定係数を含む3元連立方程式の解 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




Rimg0010 連立方程式を解くウィルバーマシン Masakazu Takahashi Flickr
最初は、問題の連立方程式をそのまま書くよね」 ユーリ 「書いたよ」 $$ x y = 5 \\ 2x 4y = 16 $$ 僕 「いやいや、連立方程式を解いてみせるんだから、こんなふうに書くといいんだよ」 左側に中かっこ( $\{$ )を書いて、まとまりを表す。抵抗に関する連立方程式を解く必要がある。そこで,「キルヒホッフの法則」を説明する前に,ここ では数学的な準備として,未知数が二つの2 元連立1 次方程式と変数が三つの3 元連立1 次方程式に ついて,クラーメルの公式による解法を説明する。 1連立方程式とパラメータ 前回習った方法(基本変形) を次の方程式に適用すると, 係数行列を単位行列まで 変形できない 例31 連立方程式 (x2y = 2···⃝1 2x4y = 4···⃝2 ···(♡) の拡大係数行列A˜ に対し, A˜ = 1 2 2 2 4 4 ⃝2 −2×⃝1 −−−−−−→ 1 2 2 0 0 0




大家來解謎 解二元一次聯立方程式 導入活動 環遊數界




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
3 連立一次方程式の基本変形 定義 28(連立一次方程式の基本変形) 連立一次方程式に対する次のの操作を連立一次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加える. 連立一次方程式に基本変形をして得られた方程式と元の方程式とは等価な方程式である.2つの文字 が含まれている連立方程式を解くには,加減法や代入法を使って,どちらか一方の文字を消去し,1つの文字だけの方程式に直して解くようにします. この問題のように の係数がそろっているときは,左辺どうし,右辺どうしを引くと を消去することができます.




連立方程式の解法 13 08 17 連立方程式の解法連立方程式をエクセルを用いて解く方法は以下の2種類が考えられます




連立方程式の解き方 電験3種web




連立3元1次方程式 身勝手な主張



連立方程式計算 Apps On Google Play



名師課輔網 係數對稱的聯立方程式




國一數學 二元一次聯立方程式by 林國源校長均一 國中數學basic Education




ある連立3元3次方程式を解いてみよう 身勝手な主張




三元一次連立方程式を一発で解く方法 Geogebra




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



3 1進階01指數聯立方程式 指數 均一教育平台




1 3 2 1 4 2 2 15r




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




中2数学 連立方程式の文章題 基礎 練習編 映像授業のtry It トライイット



連立方程式 行列計算for Android Apk Download
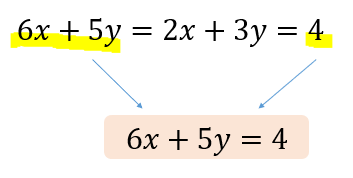



連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト




連立方程式計算安卓下载 安卓版apk 免费下载




3 Begincases2x 3y263y 5x2en See How To Solve It At Qanda
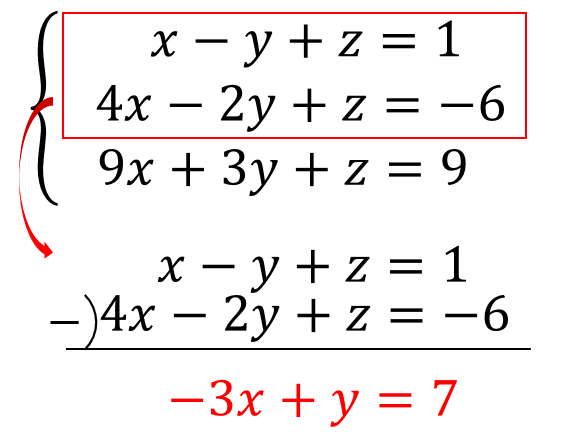



最も共有された 三連立方程式 犬イラスト




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




連立方程式 3つの文字 式の問題を計算する方法は 数スタ



Q Tbn And9gcrnu5a5m1hrhxj0x2t Oun9obnfyeyhai5yymirard 78t6nw Usqp Cau




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




國二junior High数学的連立方程式 筆記 Clear
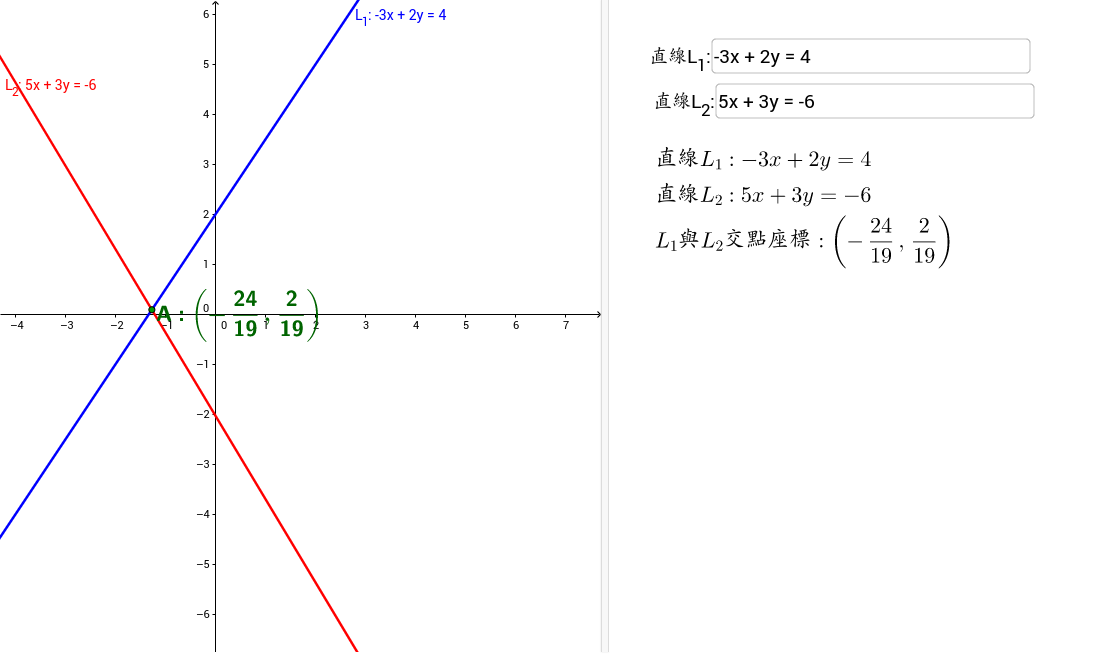



二元一次聯立方程式圖解 Geogebra



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf



第1章 連立方程式



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 3 1 E7 9a E6 80 E6 96 B9 E7 A8 8b E7 B5 84 E8 87 E7 9f E9 99 A3 E4 Bf Ae E8 A8 Pdf



Q Tbn And9gcsm6 Ygdifx7pydebyfkxkcficln0q2usbh7vlhkbagbczf8kws Usqp Cau




翻轉學習影片 國中 數學 4 2 2 解二元一次聯立方程式




連立方程式の利用の問題の解き方 代金の問題 1 現役塾講師のわかりやすい中学数学の解き方




中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット



Http Www Math Nsysu Edu Tw Outstanding Use Report 1007 Pdf




二元一次聯立方程式的圖形 劉繼文 新泰國中 Shareclass




25 3 連立方程式 ニスヌーピー壁紙




Intro Linear Note




求解 這兩題我不會 Clear




二元一次聯立方程式的基礎概念 均一教育平台




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook




Ok423 三元一次連立方程組1 Ok423 三元一次聯立方程式主題一解聯立方程式1 可用加減消去法或代入消去法求解 2 聯立方程式的解可分成三種 1 恰有一解 2 無限多組解 3 無解 Pdf 免费下载




連立方程式の解法 13 08 17 連立方程式の解法連立方程式をエクセルを用いて解く方法は以下の2種類が考えられます




1 3 2 1 4 2 2 15r




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook



Http Www Topmath Org J Student Pdf




中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット




方程式計數機連立一次方程式の計算機 Cpdpg




二元一次聯立方程式的應用題3 二元一次聯立方程式的應用問題 均一教育平台
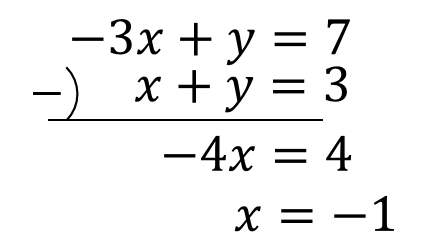



連立方程式 3つの文字 式の問題を計算する方法は 数スタ




求高手我這三題真的無法這是二元一次聯立方程式應用覺得難 Clear



解二元一次聯立方程式 代入消去法 Live 多媒體數學觀念典online



Q Tbn And9gctgoae9bomuk0gymqhrkjzep3izucoijhp9evjmecua8k 13ra4 Usqp Cau



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf
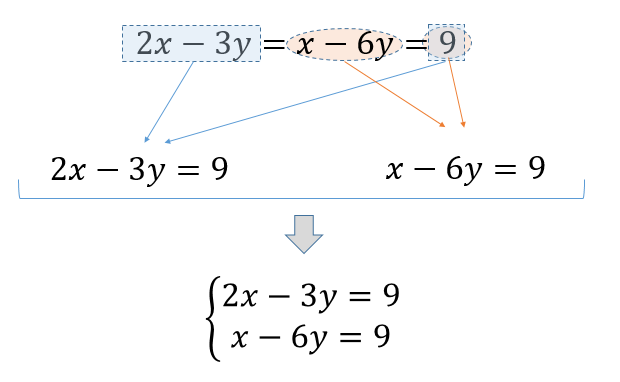



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




建宏國中e把罩數學 3 二元一次聯立方程式



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




追車子 3
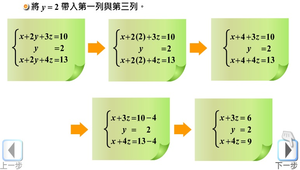



高斯消去法解三元一次聯立方程式



3 元 2 次 方程式




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学



加減




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




例題 加減消去法2 數學 均一教育平台



三元一次方程式求連比 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌




翻轉學習影片 國中 數學 直角坐標平面與二元一次方程式圖形 二元一次聯立方程式的圖形



1




連立方程式で3つの式のある3元1次方程式とは 3元連立方程式の解き方をわかりやすく解説 Himokuri




トップ100連立方程式公式 最高のカラーリングのアイデア




高二高中數學的 數甲 B4 2 3 三元一次聯立方程式筆記 Clear



3乗の連立方程式が解けません 宜しければ解き方教え Yahoo 知恵袋




連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト



連立方程式の行列解
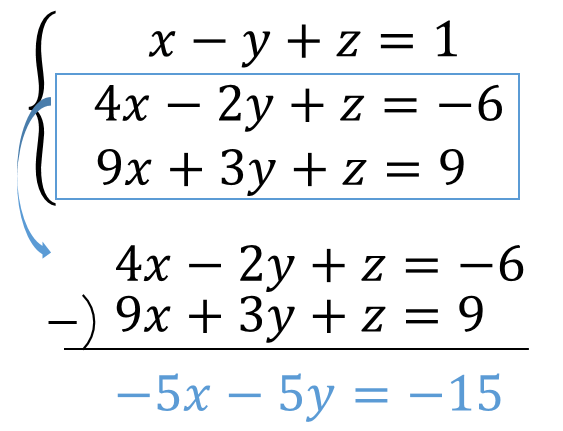



連立方程式 3つの文字 式の問題を計算する方法は 数スタ




高校数学 3つの解から3次方程式の作成 3変数対称式の連立方程式 受験の月




連立3元1次方程式 まなびの学園




例題 連立3元1次方程式の解き方 Youtube




第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download




連立方程式 3つの文字 式の問題を計算する方法は 数スタ




整数解をもつ連立3元2次方程式を解こう 2017年度前期日程の一橋大学入試問題 身勝手な主張




二元二次方程式定義連立方程式とは Gjlni




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
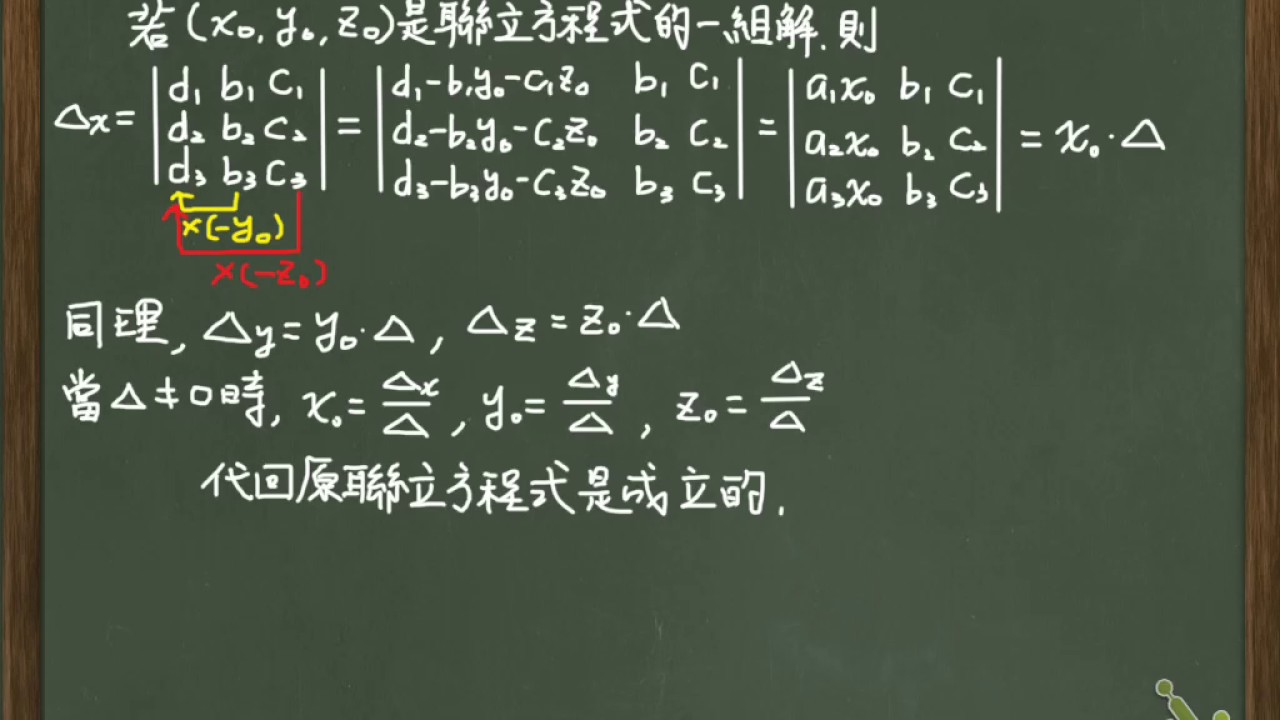



40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Youtube



三元一次聯立方程式 解三元一次方程組 Youtube




連立方程式の解き方 加減法 1 Youtube




連立方程式 3 応用編1 Youtube




怎麼知道的 紅線 Clear




隨筆誌 二下2 3三元一次聯立方程式比例式解題想法




均一影片 例題 解二元一次聯立方程式 綜合應用3 學習單 Shareclass



0 件のコメント:
コメントを投稿