解説 これでわかる! 例題の解説授業 x 2 +(a+b)x+ab=(x+a)(x+b) のカタチに因数分解する問題だね。 POINT 解くコツは 1.(x+ )(x+ )をイメージ 2.「 と のかけ算」は右端になる 3.「 と のたし算」はxの係数になる中3数学 いろいろな因数分解 目次 例題 共通因数→乗法公式 例題 置き換えの因数分解 練習問題 プリントを印刷,ダウンロード(PDFファイル)多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式 (xa) (xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_ (xa) (xb) 因数分解3_2乗 因数分解4_ (xa) (xa) 因数分解 おきかえ 共通因数をくくりだした後さらに因数分解 項を分けて因数分解する1 (発展) 項を分けて因数分解

高校入試 難関校の因数分解を解説 Youtube
因数分解 例題 高校
因数分解 例題 高校-因数分解の簡単な解き方がわかる3つのステップ 因数分解のやり方は3ステップさ。 っていわれてもわからんよね? ? 今日はいっしょに例題をといてみよう。 つぎの多項式を因数分解してください。 やり方1 共通因数をくくりだす まず共通因数を数 学 i 式の展開と因数分解 例題(8) 練習問題 練習問題+解答al教材計算の工夫 al教材計算の工夫(解答) 実数,1次不等式 例題(11) 練習問題 練習問題+解答集合と論理 例題(6) 練習問題 練習問題+解答




因数分解のいろいろな計算 無料で使える中学学習プリント
例題1 次の式を因数分解してください. 因数定理を使って因数分解するには,与えられた整式を とおいて,適当な整数 に を代入して,ちょうど0になるものを探します.この問題を a について整理しても間違いではありませんが,2次式の因数分解になるので次のようにやや複雑になります. axbxa 2 −b 2 =a 2 xa−b 2 bx この2次式を因数分解するには,積が −b 2 bx になるものうちで,和が x になるもの と を探して (a )(a )== 3次以上の因数分解 == (例題→選択問題) ※ 3次以上の式の因数分解を行う強力な方法として「因数定理」があるが,これは数学iiで習う.数学iではもっと簡単に「因数分解公式」「置き換え」などで因数分解できるものだけを扱う.
因数分解の例題 具体的な因数分解の問題の解き方ですが、さきに結論を言いますと どの公式に当てはまるか を考えることを常にしてください。具体的には与えられた問題が先ほど紹介しました公式①〜⑧のどれに当てはまるかを考えることです。素数・素因数分解 素数 約数が1と自分自身の2つしかない自然数のことを 素数 という。 次の数のうち素数はどれか。 6, 5, 1, 0 6の約数は1,2,3,6の4つあるので6は素数ではない。 5の約数は1,5の2つだけなので5は素数である。(ab)が負でabが正のときの因数分解 例 x 2 8x12 の因数分解 x2 8x12 = (x □) (x △)
6 やりがちなミス どの項目も、平等に分解してしまう 61 ツリーのバランスの良さと、合理的なプロセスは関係ないTry IT(トライイット)の因数分解の公式1 (x+a)(x-a)の逆の例題の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。例題 例題1 次の式を因数分解せよ. (1) 12xy3 −27x3y 12 x y 3 − 27 x 3 y (2) 6x2 x−1 6 x 2 x − 1 (3) 16a3 54b3 16 a 3 54 b 3 (4) (x2 −2x)2 −11(x2 −2x) 24 ( x 2 − 2 x) 2 − 11 ( x 2 − 2 x) 24 (5) x(x−1)(x−2)(x−3)−24 x ( x − 1) ( x − 2) ( x − 3) − 24 (6)




数学 因数分解チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru




高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月
1つの文字で整理する因数分解: 説明 ・ 例題 ・ 練習問題 対称式・交代式の因数分解: 説明 ・ 例題 ・ 練習問題 複2次式の因数分解: 説明 ・ 例題 ・ 練習問題 公式を利用した高次方程式の因数分解: 説明 ・ 例題 ・ 練習問題 数学Ⅰの目次へ 数学の解答 これは, 因数分解公式(n乗の差,和) で紹介したように, x 5 − 1 = ( x − 1) ( x 4 x 3 x 2 x 1) x^51= (x1) (x^4x^3x^2x1) x5 − 1 = (x− 1)(x4 x3 x2 x1) と分解できる。 ここで, 厳密には f ( x) = x 4 x 3 x 2 x 1 = x 5 − 1 x − 1 f (x)=x^4x^3x^2x1=\dfrac {x^51} {x1} f (x) = x4 x3 x2 x 1 = x −1x5 −1実は、 数字も考えないといけない。 9は3×3、6は2×3だから、以下のようになる。 9ab-6bc = 3×3×a×b-2×3×b×c = 3b ( 3a-2c ) ・・・答 (3) ab2 a2b ab 全部の項に ab が入っている。 ab2 a2b ab = ab(b a 1) ・・・答 abの項は共通因数でくくると1になる 。




2元2次式の因数分解 例題で学ぶ高校数学



因数分解例題解答 Of 京極一樹の数学塾会員頁
例題6.x 2 10x25を因数分解しなさい。 上記の例題の場合、真ん中の項は10なので2で割ることが可能です。 10を2で割ると5となりますが、この答えを二乗して右の項と同じになれば先述の公式3に当てはめて解答することが可能です。高校1年 数学i 因数分解予習用練習問題 数学Ⅰ目次 ブログトップ;4 例題: とあるカフェ1店舗の売上金額は? 5 Step1 目的数値(売上金額)を因数分解する;




高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ




因数分解 の問題のわからないを5分で解決 映像授業のtry It トライイット
今回は、難関高校の入試に出題された因数分解の難問を解説していきます。 因数分解は、必ず取りたい問題の1つです。 実際に出題された問題から抜粋して紹介しているので これらの問題を全部解けるようになれば、本番もバッチリのはず!== 因数分解の入試問題 == 引用元の問題は記述式の問題ですが,以下の問題ではWeb画面上での操作性をよくするため,選択問題に変えています. まぐれ当たりでは力が付きませんので,計算用紙を使って,よく考えてから選択肢の内の1つをクリックして微分作用素の因数分解 一般解 複素数値解から実数値解へ 例題 応用例 微分作用素の因数分解 u′ u = (d dt )u と書いて, (d dt ) を微分作用素 と呼ぶ このとき, 特性方程式の因数分解 2 a b = (1)(2) に付随して, 2階の微分作用素が1階の微分作用素の積



1




高校入試 難関校の因数分解を解説 Youtube
多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式 (xa) (xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_ (xa) (xb) 因数分解3_2乗 因数分解4_ (xa) (xa) 因数分解 おきかえ 共通因数をくくりだした後さらに因数分解 項を分けて因数分解する1 (発展) 項を分けて因数分解因数分解 例題集 Q 1 次の式を因数分解しなさい。 (1) x 3 y 5 x 4 y 2 (2) x 3 y 5 z 8 x 4 y 6 z 2 − x 6 y z 4 (3) x y − x − y 1 解答・解説を見る (1) x 3 y 2 ( y 3 x)複素数の範囲での因数分解の例題4問 与えられた多項式を「 の範囲で因数分解する」とは, 係数の多項式の積に(できるだけ細かく)分解するという意味。 因数分解の問題で特に指示がない場合は「整数の範囲で」因数分解すればOKですが,この記事では複素数の範囲での因数分解について考えます。




例題で学ぶ高校数学 2元2次式の因数分解




3次式の因数分解 公式とやり方について問題を使って解説 数スタ
→複二次式の因数分解のやり方と例題5問 ~おまけ、その他の公式~ $x^ny^n$ $=(xy)(x^{n1}x^{n2}y\cdots xy^{n2}y^{n1})$ ($n$ 乗の差は因数分解できる) $x^{2n1}y^{2n1}$ $=(xy)(x^{2n}x^{2n1}y\cdots xy^{2n1}y^{2n})$ (奇数乗の和は因数分解できる) $a^3b^3c^33bac$32 例題③ の解き方 4 たすきがけの因数分解のやり方まとめ 数学ⅡBの3次式の因数分解の公式 東大塾長の山田です。 このページでは、 「 たすきがけの因数分解のやり方 」について解説します 。 具体的に例題を使って、丁寧に解説しています。 また、 「因数分解の問題が絶対に解けるようになる、因数分解の手順」 と、 「いつたすきがけを使えばいいか因数分解 (降べきの順に整理) 因数分解せよ x 2 y 2 3xz3yz 説明 x、yについて2次式、zについて1次式なので 次数の低いz について降べきの順に整理する。 x2y23xz3yz = 3 (yx)zx 2 y 2 = 3 (yx)z (xy) (xy) = 3 (xy)z (xy) (xy) = (xy) (xy3z) x 3




因数 分解 解 の 公式 因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Amp Petmd Com



1
因数分解(基本問題2) 次の式を因数分解しなさい ax 23a 12a 3 4a 4ax 2 6a x 2 7x12 x 2 15x56 x 2 6x9 次の式を因数分解しなさい x 2 11x30 x 212x x 23x2 x 216x64 x 21 x 2y 2 次の式を因数分解しなさい x 2 4x5 x 23x4 x 2x6 x 22x8 x 24x12 x 2 24x144この記事では「(1)因数分解を使うタイプ」の問題について紹介していきたいと思います。 整数問題を因数分解を使って解く 例題$\ n\ $が2以上の素数でない整数ならば、$\ 2^n1\ $も素数でないことを示せ。例題 練習問題 定理・公式の証明 補足;
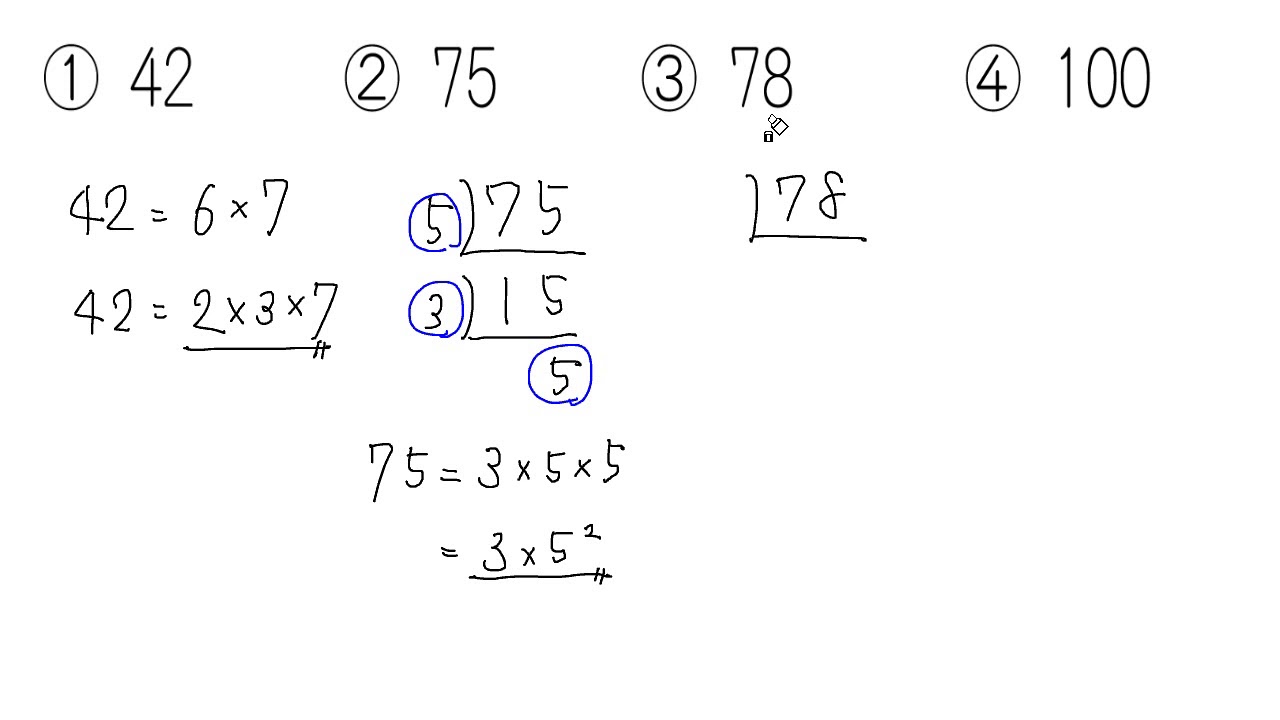



素因数分解 問題 Youtube




中学数学 因数分解の解き方と練習問題 Irohabook
共通因数をくくり出した後、 さらに因数分解 する 例12ax 2 18a の因数分解 2ax 2 18a = 2a (x 2 9) ←2aをくくりだす = 2a (x3) (x3) ←かっこの中を因数分解 例2 6x 2 y6xy36y の因数分解 6x 2 y6xy36y = 6y (x 2 x6) ←6yをくくりだす = 6y (x3) (x2) ←カッコの中を因数分解 必ず 先に共通因数をくくりだす。整式を因数分解するために,共通因数があればまずそれを括り出します. 例題 x の整式3x2−9x6 を因数分解する. 3 を括り出す. 3x2−9x6=3(x2−3x2)=3(x−1)(x−2) 終 例題 tの整式 3−32−4 を因数分解する. 共通因数t を括り出す.




改訂版 3trial数学 P14 3 因数分解 練習問題



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス




高校入試 難関校の因数分解を解説 Youtube
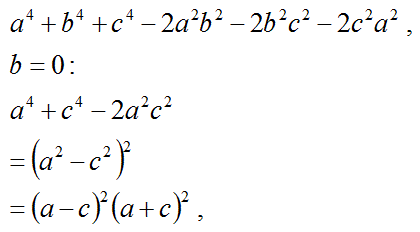



勉強しよう数学解答集 因数分解の応用問題の問2の解答




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス




1 Ab Ab Ca Ca 2a Descubre Como Resolverlo En Qanda




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す




因数分解の解き方と問題 応用 Irohabook




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解
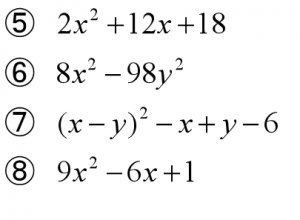



因数分解に慣れよう 後編 インターネット家庭教師のアスミラ




因数分解 おいしい数学
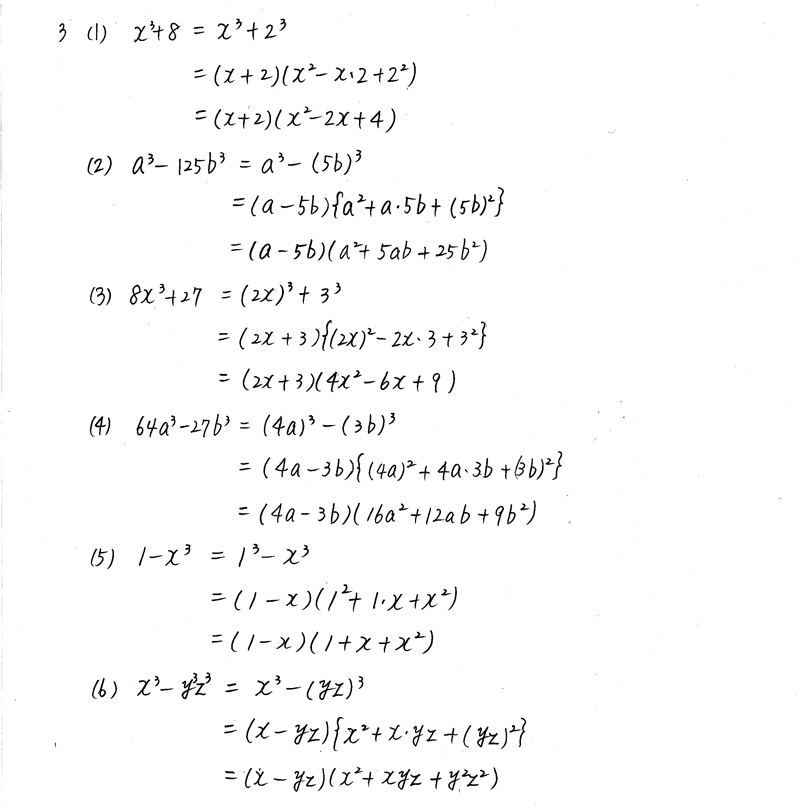



新課程 3trial数学 P6 1 3次式の展開と因数分解




因数分解の解き方や問題 中学3年生の方は 必見 三重の個人契約家庭教師




中学数学 多項式 の教え方 因数分解の応用問題




高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ



Studydoctor x a x b の因数分解 中3数学 Studydoctor




無料 中3数学 発展 応用問題 問題プリント 305 式の計算5 因数分解1



U9j580gf8iba369ji2w Xyz P 599




無料 中3数学 標準問題 問題プリント 306 式の計算6 因数分解2




無料 中3数学 基本問題 問題プリント 305 式の計算5 因数分解1




例題 演習問題付き 公式では解けない 因数分解の4つの対処法をご紹介し




3分で分かる 因数分解の公式と解き方のコツ 練習問題と解説をわかりやすく 合格サプリ




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解




素因数分解 無料で使える中学学習プリント




高校数学 因数分解 複素数が登場する因数分解の方法 数学の面白いこと 役に立つことをまとめたサイト



高校数学因数分解 この問題がわかる方教えてください Yahoo 知恵袋




因数分解 練習問題 清水塾




無料 中3数学 基本問題 問題プリント 304 式の計算4 素因数分解




数学 質問解答 3文字 の因数分解 パート1 高校数学 数a 因数分解 質問ありがとうございました 行間 ぎょうのあいだ 先生




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 因数分解の解き方と練習問題 Irohabook
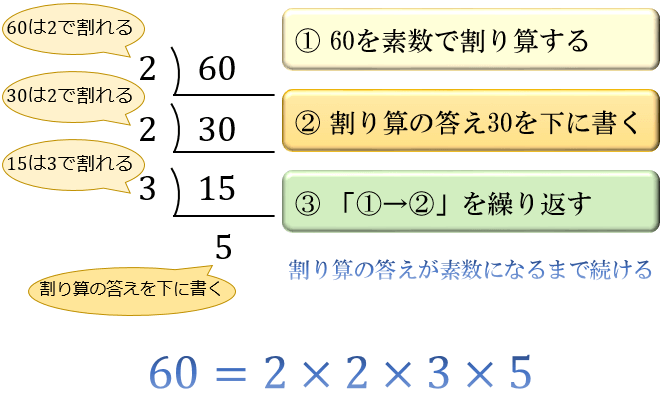



素因数分解のやり方 5つのステップで分かる素因数分解問題の解き方とコツ アタリマエ




因数分解のいろいろな計算 無料で使える中学学習プリント



U9j580gf8iba369ji2w Xyz P 608




中学3年数学 因数分解 因数分解をわかりやすく解説 高校入試出題率100 数学の面白いこと 役に立つことをまとめたサイト




因数分解の公式のまとめ 中学生はこのパターンを覚えておこう 中学や高校の数学の計算問題




中学 数学 因数 分解 シモネタ




因数分解 練習問題1 選択mba ロジカルシンキング 練習問題 トレーニング 例題 テスト Mece




たすきがけの因数分解のやり方 問題付き 理系ラボ
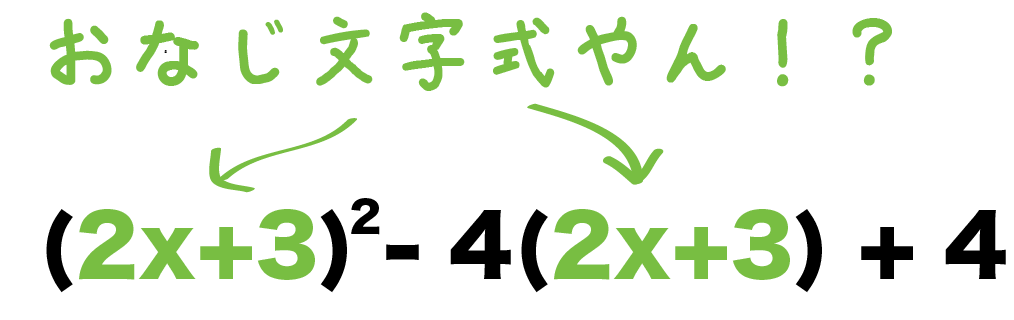



いろいろな因数分解 置き換え問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



高校数学1の因数分解の応用編の問題なのですが 下の写真の 2 と 3 の Yahoo 知恵袋
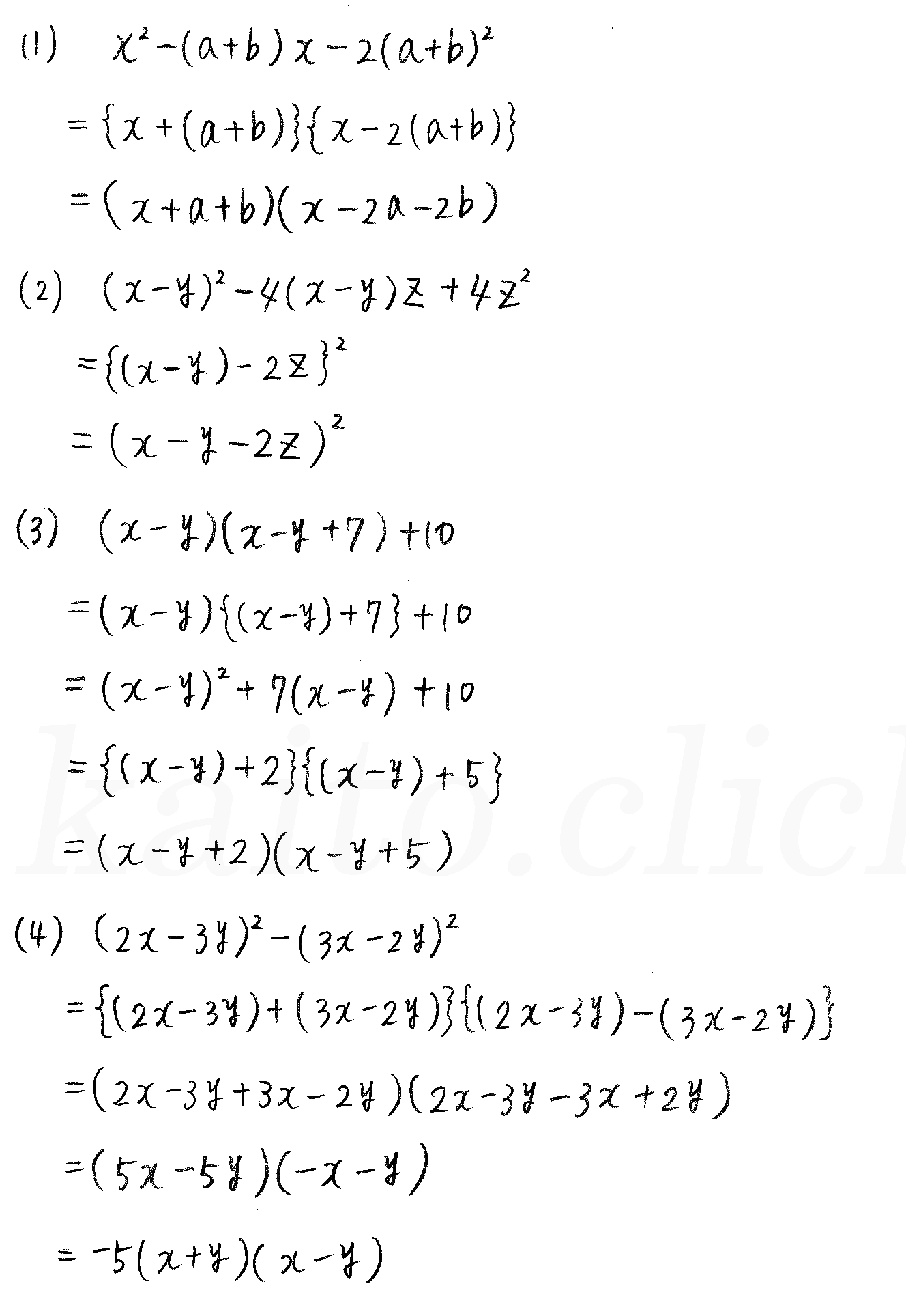



改訂版 クリアー数学 P15 5 因数分解 2




高校入試 難関校の因数分解を解説 Youtube



面白クイズ 9991を素因数分解




高校数学 因数分解公式と3次式の因数分解 受験の月
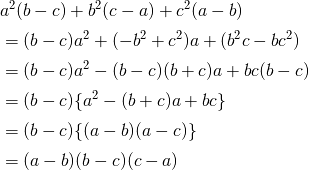



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局




因数分解の公式まとめ一覧とその活用例 アタリマエ




因数分解難問と意外な別解 怜悧玲瓏 高校数学を天空から俯瞰する




モノマナビ研究所




因数定理を利用した因数分解の練習問題 高校数学の知識庫



因数 分解 コツ 複雑な式の因数分解 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション Amp Petmd Com




中学生向け 因数分解の問題を解く2つのチェックポイント 京橋数学塾a4u




無料 中3数学 基本問題 解答プリント 305 式の計算5 因数分解1




74 46 2 1 9 2 2 3 X22x Lihat Cara Penyelesaian Di Qanda



1




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Studydoctor素因数分解のやり方 中3数学 Studydoctor




素因数分解とは 素因数分解のやり方を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ




展開 因数分解の利用 図形 清水塾




中3 数学 因数分解 共通因数でくくる 無料学習プリント教材



置換因数分解例題 京極一樹の数学塾




素因数分解の応用問題の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



因数分解の意味 問題の解き方 数学fun




複素数の範囲で因数分解しろって言う問題なんですけど2番はiがでてくるから複素数の範囲 Clear




中学3年の数学 動画 因数分解 もっと応用編の問題 19ch




3乗の因数分解 展開 公式 理系ラボ
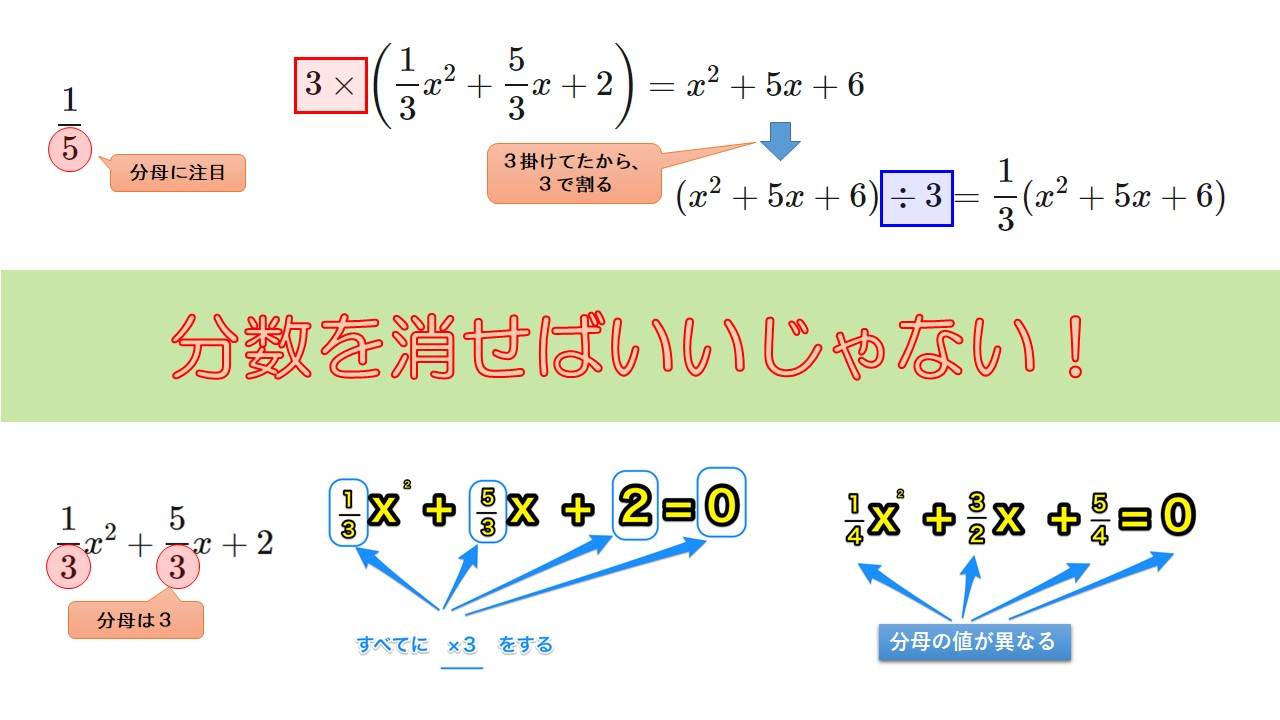



高校数学 因数分解 分数が登場する式を因数分解する方法 わかりやすく解説します 数学の面白いこと 役に立つことをまとめたサイト




今年も因数分解コンクール 最近の出来事 英国 イギリス留学生へのキリスト教に基づく全人教育 立教英国学院 Rikkyo School In England




解けますか ちょっと難しい因数分解 暇つぶしに動画で脳トレ



因数分解とは 公式や計算のやり方 問題の解き方 受験辞典



因数分解とは 公式や計算のやり方 問題の解き方 受験辞典




因数分解 8 交代式の因数分解 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 長い式の因数分解2 例題編 映像授業のtry It トライイット




因数分解の応用問題の解き方 現役塾講師のわかりやすい中学数学の解き方




好き の因数分解 Amazon Com Books




数学 質問解答 高校生の因数分解2 2つの文字を含んだ式 高校数学 数a 因数分解 行間 ぎょうのあいだ 先生
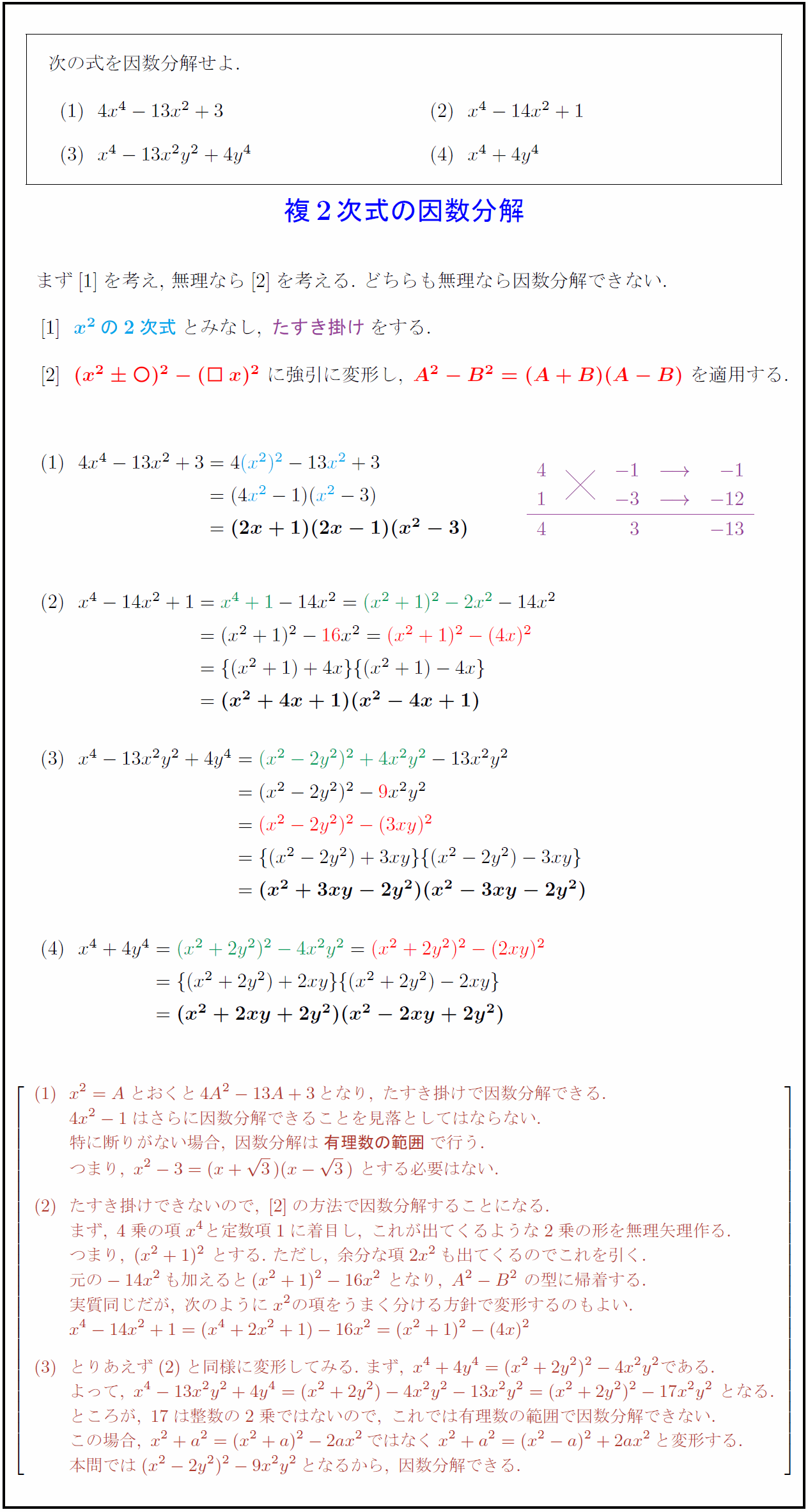



高校数学 複2次式 2乗の2次式ax Bx C の因数分解 受験の月




因数分解の例題解説 ぼーの秘密部屋



因数分解とは 1分でわかる意味 公式の一覧 問題 たすきがけのやり方



素因数分解が難しい日付19選 素数選 Sosu Lover Number Mania Note




数学iの因数分解について質問です Clear




二次方程式 因数分解を利用した解き方を例題解説 数スタ




因数分解 これが解けたらすごいよ 苦手な数学を簡単に




高校1年 数学i 因数分解 予習用練習問題 赤城 ᐡᐤᐡ




中3 式の計算 因数分解 応用編 基本の理解で組立ok 難問と勉強の取組みについて 教えたい 人のための 数学講座



素因数分解のドリル



1



Studydoctor2乗の因数分解 中3数学 Studydoctor




高校数学 因数分解 基本問題 16年3月15日 Youtube



0 件のコメント:
コメントを投稿